网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设L为球面x^2+y^2+z^2=1与平面x+y+z=0的交线,则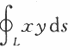 =_________.
=_________.
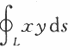 =_________.
=_________.参考答案
参考解析
解析:利用第一类曲线积分的轮换对称性.


更多 “设L为球面x^2+y^2+z^2=1与平面x+y+z=0的交线,则=_________.” 相关考题
考题
一平面通过两点M1(1,1,1),M2(0,1,-1),且垂直于平面x+y+z=0,则它的方程为( )。
A.2x+y-z=0
B.2x-y+z=0
C.x-y-z=0
D.2x-y-z=O
考题
球面x2 + y2 + z2 = 9与平面x + z = 1的交线在xoy坐标面上投影的方程是:
(A) x2 + y2 + (1-x)2 = 9
(C) (1-z)2 + y2 + z2 = 9
考题
过点(1,0,0),(0,1,0),且与曲面z=x^2+y^2相切的平面为
A.Az=0与x+y-z=1
B.z=0与2x+2y-z=2
C.x=y与x+y-z=1
D.x=y与2x+2y-z=2
考题
单选题在平面x+y+z-2=0和平面x+2y-z-1=0的交线上有一点M,它与平面x+2y+z+1=0和x+2y+z-3=0等距离,则M点的坐标为( )。A
(2,0,0)B
(0,0,-1)C
(3,-1,0)D
(0,1,1)
考题
单选题关于投影的说法正确的是()A
平面与球面截交线的投影是圆B
平面与球面截交线的投影是直线C
平面与球面截交线的投影是椭圆D
平面与球面截交线不可能是椭圆
热门标签
最新试卷