网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知矩阵A=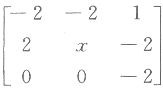 与B=
与B= 相似.
相似.
(Ⅰ)求x,y;
(Ⅱ)求可逆矩阵P使得P^-1AP=B.
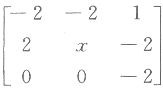 与B=
与B= 相似.
相似.
(Ⅰ)求x,y;
(Ⅱ)求可逆矩阵P使得P^-1AP=B.
参考答案
参考解析
解析:



更多 “已知矩阵A=与B=相似. (Ⅰ)求x,y; (Ⅱ)求可逆矩阵P使得P^-1AP=B.” 相关考题
考题
填空题麦肯锡矩阵原理和基本思想与()相似,都能适用于()的战略分析,麦肯锡矩阵使用了更多的因素来()。
热门标签
最新试卷