设A为n阶实对称矩阵,下列结论不正确的是().A.矩阵A与单位矩阵E合同B.矩阵A的特征值都是实数C.存在可逆矩阵P,使P^-1AP为对角阵D.存在正交阵Q,使Q^TAQ为对角阵
设(X,Y)的联合密度函数为f(x,y)= (1)求a;(2)求X,Y的边缘密度,并判断其独立性;(3)求.
设随机变量(X,Y)的联合密度函数为f(x,y)=(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
设矩阵的特征方程有一个二重根,求的值,并讨论A是否可相似对角化
设随机变量X,y相互独立,且X~P(1),y~P(2),求P(max{X,Y}≠0)及P(min{X,Y}≠0).
设矩阵相似于矩阵. (1)求a,b的值;(2)求可逆矩阵P,使为对角阵
设随机变量(X,Y)的联合密度为f(x,y)=求: (1)X,Y的边缘密度;(2)P
设X,y的概率分布为X~,Y~,且P(XY=0)=1. (1)求(X,Y)的联合分布;(2)X,Y是否独立?
设X,Y相互独立,且X~B,Y~N(0,1),令U=max{X,Y},求P{1
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3. 设随机变量U=max{X,Y},V=min{X,Y}. (1)求二维随机变量(U,V)的联合分布;(2)求Z=UV的分布; (3)判断U,V是否相互独立?(4)求P(U=V).
设随机变量X~E(λ),令Y=,求P(X+Y=0)及FFY(y).
设A=,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.
设矩阵A= (1)已知A的一个特征值为3,试求y; (2)求可逆矩阵P,使(AP)^T(AP)为对角矩阵.
已知矩阵A=与B=相似. (Ⅰ)求x,y; (Ⅱ)求可逆矩阵P使得P^-1AP=B.
设二维离散型随机变量(X,Y)的概率分布为 (Ⅰ)求P{X=2Y); (Ⅱ)求Cov(X-Y,Y).
设随机变量X与Y的概率分布分别为, 且P{X^2=Y^2}=1. (Ⅰ)求二维随机变量(X,Y)的概率分布; (Ⅱ)求Z=XY的概率分布; (Ⅲ)求X与Y的相关系数ρXY.
设随机变量X的概率密度为令随机变量, (Ⅰ)求Y的分布函数; (Ⅱ)求概率P{X≤Y}.
设随机变量X与Y相互独立,X的概率分布为P{X=1}=P{X=-1}=,Y服从参数为λ的泊松分布.令Z=XY. (Ⅰ)求Cov(X,Z); (Ⅱ)求Z的概率分布.
设随机变量X,Y相互独立,且X的概率分布为P{X=0)=P{X=2)=,Y的概率密度为 (Ⅰ)求P{Y≤EY}; (Ⅱ)求Z=X+Y的概率密度.
X为3阶随机矩阵,分别对X进行如下操作: 求X的三角分解;求X的正交分解;求X的特征值分解;求X的奇异值分解;
设A,B都是n阶矩阵,若有可逆矩阵P使得P-1AP=B,则称矩阵A与矩阵B()。A、等价B、相似C、合同D、正交
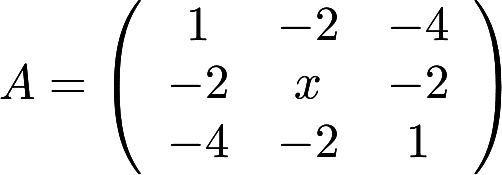 与
与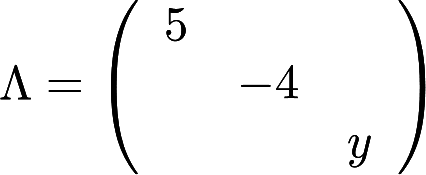 相似,求x, y,并求一个正交阵P,使
相似,求x, y,并求一个正交阵P,使 。
。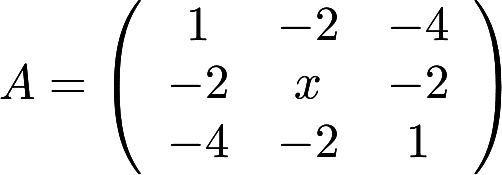 与
与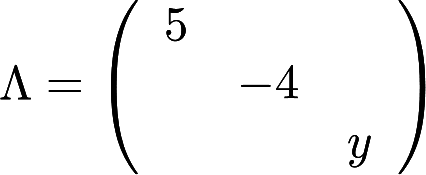 相似,求x, y,并求一个正交阵P,使
相似,求x, y,并求一个正交阵P,使 。
。
