网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
离散型随机变量的概率分布为P(X=K)=(K+1)/10,K=0,1,2,3,则E(X)为( )。
A.2.4
B.1.8
C.2
D.1.6
B.1.8
C.2
D.1.6
参考答案
参考解析
解析: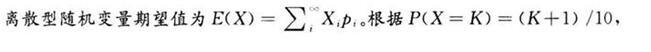
得:P(X=0)=1/10,P(X=1)=2/10,P(X=2)=3/10,P(X=3)=4/10。所以,E(X)=0×1/10+1×2/10+2×3/10+3×4/10=2。
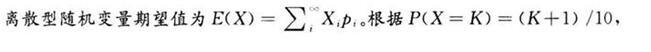
得:P(X=0)=1/10,P(X=1)=2/10,P(X=2)=3/10,P(X=3)=4/10。所以,E(X)=0×1/10+1×2/10+2×3/10+3×4/10=2。
更多 “离散型随机变量的概率分布为P(X=K)=(K+1)/10,K=0,1,2,3,则E(X)为( )。A.2.4 B.1.8 C.2 D.1.6 ” 相关考题
考题
单选题若某人群某疾病发生的阳性数X服从二项分布,则从该人群中随机抽出n个人,阳性数X不少于k人的概率为()。A
P(k+1)+P(k+2)+…+P(n)B
P(0)+P(1)+…+P(k)C
P(0)+P(1)+…+P(k+1)D
P(k)+P(k+1)+…+P(n)E
P(1)+P(2)+…+P(k)
考题
问答题9.设离散型随机变量X的分布律为 求x的分布函数,以及概率P{1.50.5}.
热门标签
最新试卷