微分方程y-y=0满足y(0)=2的特解是( )。
微分方程y-y=0满足y(0)=2的特解是( )。
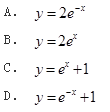
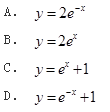
参考解析
解析:

相关考题:
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=的特解是:(A)cosy=(1+ex) (B)cosy=(1+ex) (C)cosy=4(1+ex) (D)cos2y=(1+ex)
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=π/3的特解是:A. cosy=(1/4) (1+ex) B. cosy=1+exC. cosy=4(1+ex) D. cos2y=1+ex
单选题以y1=ex,y2=e-3x为特解的二阶线性常系数齐次微分方程是( )。[2012年真题]Ay″-2y′-3y=0By″+2y′-3y=0Cy″-3y′+2y=0Dy″-2y′-3y=0
单选题微分方程cosydx+(1+e-x)sinydy=0满足初始条件y|x=0=π/3的特解是( )。Acosy=(1+ex)/4Bcosy=1+exCcosy=4(1+ex)Dcos2y=1+ex
填空题微分方程y′=ex+y满足条件y(0)=0的特解为____。