设函数y(x)是微分方程满足条件y(0)=0的特解. (Ⅰ)求y(x)； (Ⅱ)求曲线y=y(x)的凹凸区间及拐点.
设函数y(x)是微分方程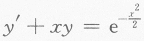
满足条件y(0)=0的特解.
(Ⅰ)求y(x)；
(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.
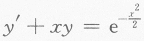满足条件y(0)=0的特解.
(Ⅰ)求y(x)；
(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.
参考解析
解析：
相关考题：
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=的特解是：(A)cosy=(1+ex) (B)cosy=(1+ex) (C)cosy=4(1+ex) (D)cos2y=(1+ex)
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=π/3的特解是:A. cosy=(1/4) (1+ex) B. cosy=1+exC. cosy=4(1+ex) D. cos2y=1+ex
设y=f（x）是微分方程y"-2y’+4y=0的一个解，又f（x0）O，f’（x0）=0，则函数f（x）在点x0（）．A、取得极大值B、取得极小值C、的某个邻域内单调增加D、的某个邻域内单调减少
单选题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（ ）。Af″（x）＋f（x）＝0Bf′（x）＋f（x）＝0Cf″（x）＋f′（x）＝0Df″（x）＋f′（x）＋f（x）＝0
单选题微分方程cosydx＋（1＋e－x）sinydy＝0满足初始条件y|x＝0＝π/3的特解是（ ）。Acosy＝（1＋ex）/4Bcosy＝1＋exCcosy＝4（1＋ex）Dcos2y＝1＋ex
单选题设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（ ）。Ax∂z/∂x＋y∂z/∂y＝0Bx∂z/∂x－y∂z/∂y＝0Cy∂z/∂x＋x∂z/∂y＝0Dy∂z/∂x－x∂z/∂y＝0
单选题函数y1（x）、y2（x）是微分方程y′＋p（x）y＝0的两个不同特解，则该方程的通解为（ ）。Ay＝c1y1＋c2y2By＝y1＋cy2Cy＝y1＋c（y1＋y2）Dy＝c（y1－y2）
单选题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（ ）。Af′（x）＋f（x）＝0Bf′（x）－f（x）＝0Cf″（x）＋f（x）＝0Df″（x）－f（x）＝0