设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ). A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同
设A,B为N阶矩阵,且A,B的特征值相同,则().A.A,B相似于同一个对角矩阵B.存在正交阵Q,使得Q^TAQ=BC.r(A)=r(B)D.以上都不对
设，当a，b为何值时，存在矩阵C使得AC-CA=B，并求所有矩阵C
设二次型. （Ⅰ）求二次型的矩阵的所有特征值； （Ⅱ）若二次型的规范形为，求的值
设3阶实对称矩阵A的各行元素之和都为3,向量都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵
设矩阵的特征方程有一个二重根，求的值，并讨论A是否可相似对角化
设A=,B=,问a,b,c为何值时,矩阵方程AX-B有解？有解时求出全部解.
设矩阵相似于矩阵. （1）求a,b的值；（2）求可逆矩阵P，使为对角阵
设矩阵且方程组无解， （Ⅰ）求a的值； （Ⅱ） 求方程组的通解
设A是三阶实对称矩阵,r(A)=1,A^2－3A=O,设（1,1,-1）t为A的非零特征值对应的特征向量.(1)求A的特征值；(2)求矩阵A.
设A，B为三阶矩阵，且满足方程.若矩阵,求矩阵B.
设，E为3阶单位矩阵（1）求方程组的一个基础解系； （2）求满足的所有矩阵B
设A=,且存在三阶非零矩阵B,使得AB=O,则a=_______,b=_______.
设矩阵A= (1)已知A的一个特征值为3，试求y; (2)求可逆矩阵P，使(AP)^T(AP)为对角矩阵.
设A是3阶实对称矩阵,满足，并且r(A)=2. (1) 求A的特征值. (2)当实数k满足什么条件时A+kE正定?
已知矩阵A=与B=相似. (Ⅰ)求x，y； (Ⅱ)求可逆矩阵P使得P^-1AP=B.
设A=，E为三阶单位矩阵. (Ⅰ)求方程组Ax=0的一个基础解系； (Ⅱ)求满足AB=E的所有矩阵B.
设矩阵，. 当a为何值时，方程AX=B无解、有唯一解、有无穷多解？在有解时，求解此方程.
设n元线性方程组Ax=b，其中 . (Ⅰ)证明行列式｜A｜=(n+1)a^n； (Ⅱ)当a为何值时，该方程组有唯一解，并求x1； (Ⅲ)当a为何值时，该方程组有无穷多解，并求通解.
设A为三阶实对称矩阵，A的秩为2，且 (Ⅰ)求A的所有特征值与特征向量； (Ⅱ)求矩阵A.
设A为3阶实对称矩阵，A的秩为2，且. （Ⅰ）求A的特征值与特征向量； （Ⅱ）求矩阵A
设A为4阶魔术矩阵，分别对A进行如下操作： 求矩阵A的逆； 求矩阵A的行列式； 求矩阵A的秩； 求矩阵A的迹；
问答题设A为4阶魔术矩阵，分别对A进行如下操作： 求矩阵A的逆； 求矩阵A的行列式； 求矩阵A的秩； 求矩阵A的迹；
，
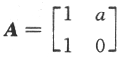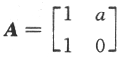，当a，b为何值时，存在矩阵C使得AC-CA=B，并求所有矩阵C.