将函数f(x）=1/(3-x)展开成(x+1)的幂级数并指出收敛区间（6分）
y=e-2x的导数为( )。A、y'=e-2xB、y'=-e-2xC、y'=-2e-2xD、y'=-2xe-2x
由曲线y=ex，y=e-2x及直线x=-1所围成图形的面积是：
设f(x)是周期为2π的周期函数，它在[-π，π]上的表达式为： 若将f(x)展开成傅里叶级数，则该级数在x=-3π处收敛于( )。
幂级数在区间(-1，1)内的和函数S(x)=________.
将函数f(x)=1-x(0≤x≤π)展开成余弦级数，并求级数的和.
设数列{an}满足条件：a0=3，a1=1，，S(x)是幂级数的和函数. (Ⅰ)证明：S"(x)-S(x)=0； (Ⅱ)求S(x)的表达式.
已知幂级数在x=0处收敛，在x=-4处发散，则幂级数的收敛域为________.
幂级数在(0,+∞)内的和函数S(x)=_________.
函数1/x展开成(x-2)的幂级数是( )。A.B.C.D.
若f(x)的一个原函数是e-2x,则∫f''(x)dx= ( )。A. e-2x+ C B. -2e-2x C.-2e-2x+C D.4e-2x+ C
将f(x)=1/(2-x)展开为x的幂级数，其收敛域为（ ）。 A. (-1,1) B. (-2,2) C.〔-1/2,1/2) D. (-∞，+∞)
将ex展开为x的幂级数，则展开式中含x3项的系数为——．
(1)将f(x)展开为x的幂级数；(2)利用(1)的结果，求数项级数的和．
将函数f(x)=xe3x展开为x的幂级数，并指出其收敛区间．
将（x-6）（x-3）（x-8）展开为系数多项式的形式。
MATLAB中提供的将函数展开为幂级数的函数是（）。A、taylorB、expandC、symsumD、float
单选题（2010）若函数f（x）的一个原函数是e-2x，则∫f″（x）dx等于：（）Ae-2x+cB-2e-2xC-2e-2x+cD4e-2x+c
问答题将（x-6）（x-3）（x-8）展开为系数多项式的形式。
单选题y″－4y＝e2x的通解为（ ）。Ay＝C1e－2x－（C2＋x/4）e－2x（其中C1，C2为任意常数）By＝C1e－2x＋（C2＋x/4）e2x（其中C1，C2为任意常数）Cy＝C1e－2x＋（C2＋x/4）e－2x（其中C1，C2为任意常数）Dy＝C1e－2x－（C2＋x/4）e2x（其中C1，C2为任意常数）
单选题若函数f（x）的一个原函数是e-2x，则∫f″（x）dx等于（ ）。[2010年真题]Ae-2x+CB-2e-2xC-2e-2x+CD4e-2x+C
填空题由于高斯投影是按带投影的，在各投影带内（）不大，（）是一微小量。故可将函数x=x（l，q），y=y（l，q）展开为（）的幂级数。
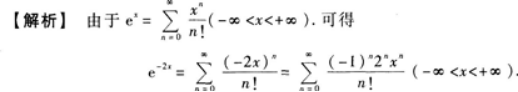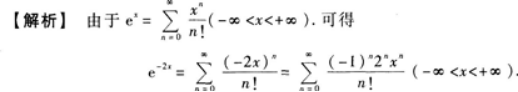【评析】将函数展开为幂级数，通常将函数与标准展开式中的函数对照．展开为幂级数之后一定要注明收敛域．