设数列{an}满足条件:a0=3,a1=1,,S(x)是幂级数的和函数. (Ⅰ)证明:S"(x)-S(x)=0; (Ⅱ)求S(x)的表达式.
设数列{an}满足条件:a0=3,a1=1,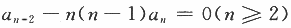 ,S(x)是幂级数
,S(x)是幂级数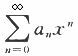 的和函数.
的和函数.
(Ⅰ)证明:S"(x)-S(x)=0;
(Ⅱ)求S(x)的表达式.
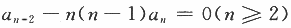 ,S(x)是幂级数
,S(x)是幂级数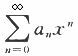 的和函数.
的和函数.
(Ⅰ)证明:S"(x)-S(x)=0;
(Ⅱ)求S(x)的表达式.
参考解析
解析:【分析】利用幂级数可逐项求导的性质,验证(Ⅰ)成立;解微分方程求出S(x),注意初值条件的使用.


相关考题:
设a是整型变量,与函数IIf(a0,-a,A.有相同结果的代数式是( )。A.B.aC.S 设a是整型变量,与函数IIf(a0,-a,A.有相同结果的代数式是( )。A.B.aC.D.-E.aF.G.aH.-a
已知数列{an}中,Sn是它的前n项和,并且Sn+1=4an+2,a1=1.(Ⅰ)设bn=an+1-2an,求证:数列{bn)是等比数列;(Ⅱ)设求证:数列{cn}是等差数列;(Ⅲ)求数列{an}的通项公式及前n项和.
设a,b是两个不相等的实数,则函数f(x)=x2+2ax+b的最小值小于零。(1)1,a,b成等差数列。(2)1,a,b成等比数列。A.条件(1)充分,但条件(2)不充分B.条件(2)充分,但条件(1)不充分C.条件(1)和(2)都不充分,但联合起来充分D.条件(1)充分,条件(2)也充分E.条件(1)不充分,条件(2)也不充分,联合起来仍不充分
单选题设随机变量X的概率密度函数f(x)=1/[π(1+x2)],则Y=3X的概率密度函数为( )。A1/[π(1+y2)]B3/[π(9+y2)]C9/[π(9+y2)]D27/[π(9+y2)]
单选题设a0,则当满足条件()时,函数f(x)=ax3+3ax2+8为增函数。Ax-2B-2Cx0Dx-2或x0