曲面x2+ y2 + z2 = 2z之内以及曲面z = X2 +y2之外所围成的立体的体积V等于:
曲面x2+ y2 + z2 = 2z之内以及曲面z = X2 +y2之外所围成的立体的体积V等于:
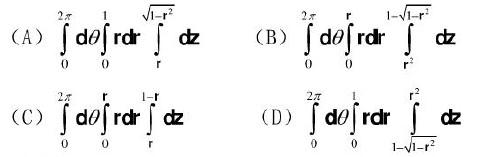
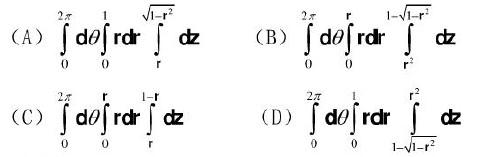
参考解析
解析:解:选D.
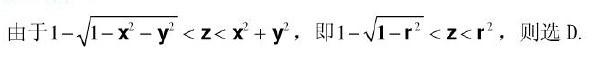
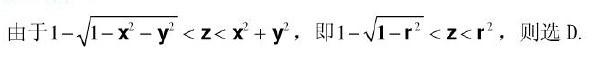
相关考题:
球面x2 + y2 + z2 = 9与平面x + z = 1的交线在xoy坐标面上投影的方程是: (A) x2 + y2 + (1-x)2 = 9(C) (1-z)2 + y2 + z2 = 9
(1)求直线y=1,曲线L以及y轴围成的平面图形绕y轴旋转一周所得到的的旋转体体积A;(2)假定曲线L绕y轴旋转一周所得到的旋转曲面为S。该旋转曲面作为容器盛满水(水的质量密度(单位体积水的重力)等于1),如果将其中的水抽完,求外力作功W.
下列关于曲面方程的结论中,错误的是()。A. 2x2-3y2-z = 1表示双叶双曲面B. 2x2+3y2-z2=1表示单叶双曲面C. 2x2+3y2-z = 1表示椭圆抛物面D. 2(x2+y2)-z2=1 表示锥面
下列关于曲面方程的结论中,错误的是()。A、2x2-3y2-z=1表示双叶双曲面B、2x2+3y2-z2=1表示单叶双曲面C、2x2+3y2-z=1表示椭圆抛物面D、2(x2+y2)-z2=1表示锥面
单选题使用Line控件在窗体上画一条从(0,0)到(600,700)的直线,则其相应属性的值应是( )。AX1=0,X2=600,Y1=0,Y2=700BY1=0,Y2=600,X1=0,X2=700CX1=0,X2=0,Y1=600,Y2=700DY1=0,Y2=0,X1=600,X2=700
单选题设z=yφ(x/y),其中φ(u)具有二阶连续导数,则∂2z/(∂x∂y)等于( )。[2017年真题]A(1/y)φ″(x/y)B(-x/y2)φ″(x/y)C1Dφ′(x/y)-(x/y)φ″(x/y)
单选题If ax + x2 = y2 -ay, what is a in terms of x and y?Ay -xBx-yCx +yD(x2 + y2)/(x + y)E(x2 + y2)/(x - y)