Ω是由曲面z=x2+y2,y=x,y=0,z=1在第一卦限所围成的闭区域,f(x,y,z) 在Ω上连续,则等于:
Ω是由曲面z=x2+y2,y=x,y=0,z=1在第一卦限所围成的闭区域,f(x,y,z) 在Ω上连续,则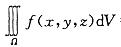 等于:
等于:
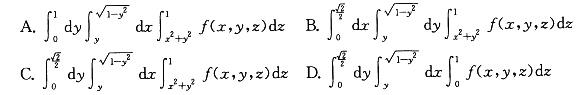
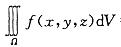 等于:
等于:
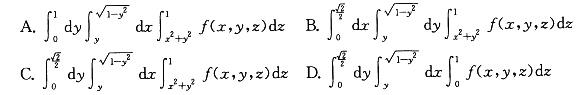
参考解析
解析:提示:作出Ω的立体图形,并确定Ω在xOy平面上投影区域:Dxy:x2+y2 = 1,写出在直角坐标系下先z后x最后y的三次积分。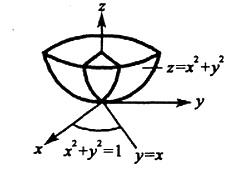

相关考题:
下列结论不正确的是()。A、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处连续B、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处可导C、z=f(x,y)在点(x0,y0)处可导,则f(x,y)在点(x0,y0)处可微D、z=f(x,y)在点(x0,y0)处偏导数连续,则f(x,y)在点(x0,y0)处连续
单选题设z=φ(x2-y2),其中φ有连续导数,则函数z满足( )。Ax∂z/∂x+y∂z/∂y=0Bx∂z/∂x-y∂z/∂y=0Cy∂z/∂x+x∂z/∂y=0Dy∂z/∂x-x∂z/∂y=0
单选题曲面z=x2+y2与平面2x+4y-z=0平行的切平面的方程是( )。A2x+4y-z-5=0B2x+4y-z=0C2x+4y-z-3=0D2x+4y-z+5=0