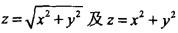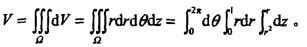立体相交通常分类有() A、平面立体与平面立体相交B、平面立体与曲面立体相交C、回转曲面体与平面立体相交D、曲面立体与曲面立体相交E、回转曲面体与非回转曲面体相交
由若干平面所围成的立体称为多面体,它的每个表面都是多边形。() 此题为判断题(对,错)。
求曲面z =2x2 +y2和z =6-x2-2y2所围立体的体积.
相贯线的空间形状与下列哪个因素没有关系( ) A两曲面立体的形状B两曲面立体的大小C两曲面立体的相对位置D两曲面立体与投影面的相对位置
回旋体时由回旋页面和回旋面与平面所围成的曲面立体。()
Ω是由曲面z=x2+y2,y=x,y=0,z=1在第一卦限所围成的闭区域,f(x,y,z) 在Ω上连续,则等于:
曲面:x2+y2+z2=2z之内及曲面z=x2+y2之外所围成的立体的体积V等于:
曲面x2+ y2 + z2 = 2z之内以及曲面z = X2 +y2之外所围成的立体的体积V等于:
( )围成的曲面体称为回转体。A.全部由曲面B.由曲面和平面共同C.由回转面D.全部由平面
( )围成的面体称为平面体。A.全部由平面B.由曲面和平面共同C.由回转面D.全部由曲面
求直线 绕 轴旋转一周的旋转曲面的方程,并求该曲面与平面所围立体的体积。
设直线L过A(1,0,0),B(0,1,1)两点,将L绕z轴旋转一周得到曲面∑,∑与平面z=0,z=2所围成的立体为Ω. (Ⅰ)求曲面∑的方程; (Ⅱ)求Ω的形心坐标.
(1)求直线y=1,曲线L以及y轴围成的平面图形绕y轴旋转一周所得到的的旋转体体积A;(2)假定曲线L绕y轴旋转一周所得到的旋转曲面为S。该旋转曲面作为容器盛满水(水的质量密度(单位体积水的重力)等于1),如果将其中的水抽完,求外力作功W.
将平面曲线y=x2分别绕y轴和x轴旋转一周,所得旋转曲面分别记作S1和S2。(1)在空间直角坐标系中,分别写出曲面S1和S2的方程;(2)求平面y=4与曲面S1。所围成的立体的体积。
x轴旋转一周,所成旋转曲面记作S。(1)在空间直角坐标系下,写出曲面S的方程;(2)求曲面S与平面x=0所围成立体的体积。
()是指表面由曲面或曲面与平面构成的几何体。A、平面立体B、空间立体C、三维体D、曲面立体
由曲面或由曲面和平面围成的立体,称为()A、棱柱体B、曲面体C、圆台体D、球体
型腔型面一般是由复杂的()等组成的腔形型面。A、立体曲面B、圆弧曲面C、过渡曲面D、线曲面
划线分为()。A、平面划线,立面划线B、平面划线,立体划线C、曲面划线,平面划线D、曲面划线,立体划线
在单组分立体相图中,若PVT状态点位于立体曲面之上,则该组分为()。
()围成的曲面体称为回转体。A、全部由曲面B、由曲面和平面共同C、由回转面D、全部由平面
被积函数f(x,y)在被积区域D上的二重积分的几何意义是:在区域D上曲面z=f(x,y)所围曲顶体的体积。
单选题表面都是由若干个平面所围成的几何形体,称为()。A正方体B多面体C平面基本体D曲面体
填空题立体分为()和()两种,所有表面均为平面的立体称为平面体,包含有曲面的立体称为曲面。
单选题立体分为平面和曲面两种,表面中包含有曲面的立体称为()。A平面体B曲面体C基本体D几何体
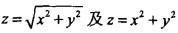 所围成的立体体积的三次积分为( )。
所围成的立体体积的三次积分为( )。

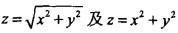 所围成的立体体积的三次积分为( )。
所围成的立体体积的三次积分为( )。

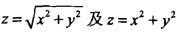 所围成的立体体积
所围成的立体体积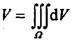 ,其中Ω为曲面
,其中Ω为曲面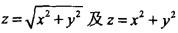
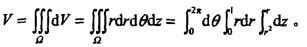
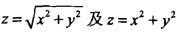 所围成的立体体积
所围成的立体体积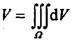 ,其中Ω为曲面
,其中Ω为曲面