设Ω是由：x2+y2+z2≤2z及z≤x2+y2所确定的立体区域，则Ω的体积等于：

设Ω是由：x2+y2+z2≤2z及z≤x2+y2所确定的立体区域，则Ω的体积等于：

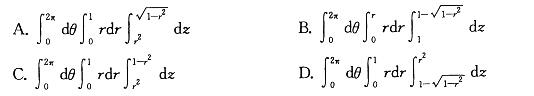
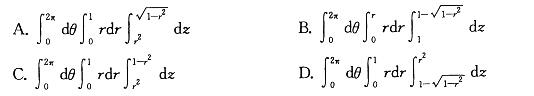
参考解析

解析：提示：本题Ω是由球面里面部分和旋转拋物面外部围成的，立体在xOy平面上投影区域：x2 +y2≤1，利用柱面坐标写出三重积分。

相关考题：

设函数z=cos(x2+y2)，则(δz/δx) _______．
查看答案
(本题满分7分)设函数z=z(x，y)由方程x2+y2+z2=xyz确定，求δz/δy。
查看答案
(本题满分8分) 设函数z=z(x，y)是由方程x+y3+z+e2x=1所确定的隐函数，求dz．
查看答案
设F是属性组U上的一组函数依赖，下列（ ）属于Armstrong公理系统中的基本推理规则。A）若X→Y及X→Z为F所逻辑蕴含，则X→YZ为F所逻辑蕴含B）若X→Y及Y→Z为F所逻辑蕴含，则X→Z为F所逻辑蕴含C）若X→Y及WY→Z为F所逻辑蕴含，则XW→Z为F所逻辑蕴含
查看答案
Ω是由曲面z=x2+y2，y=x，y=0，z=1在第一卦限所围成的闭区域，f（x，y，z） 在Ω上连续，则等于：
查看答案
曲面：x2+y2+z2=2z之内及曲面z=x2+y2之外所围成的立体的体积V等于：
查看答案
若D是由x=0，y=0，x2+y2=1所围成在第一象限的区域，则二重积分等于（　　）。
查看答案
设空间区域V：x2+y2+z2≤R2，则=( )。A、0B、1C、2D、3
查看答案
曲面x2+ y2 + z2 = 2z之内以及曲面z = X2 +y2之外所围成的立体的体积V等于：
查看答案
曲面x2+y2+z2=2z之内以及曲面z=x2+y2之外所围成的立体的体积V等于:
查看答案
设D为2≤x2+y2≤2x所确定的区域，则二重积分化为极坐标系下的二次积分时等于：
查看答案
设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．
查看答案
设函数z=z(x，y)由方程确定，其中F为可微函数，且F'2≠0，则= A.AxB.zC.-xD.-z
查看答案
设Ω是由平面x+y+z=1与三个坐标平面所围成的空间区域，则=_________.
查看答案
计算,其中Ω为z2=x2+y2，z=1所围成的立体，则正确的解法是( )。
查看答案
（）是椭球面。A、Z=（X2+Y2）/-30B、X2/100+Y2/50+Z2/40=1C、Z=X2/30D、Z=X2/100-Y3/70E、X2+Y2+Z2=100
查看答案
若序列x（n）的Z变换为X（z），则（－0.5）nx（n）的Z变换为（）A、2X（2z）B、2X（-2z）C、X（2z）D、X（-2z）
查看答案
设z=f（x2+y2），其中f具有二阶导数，则等于（）．A、2f’（x2+y2）B、4x2f"（x2+y2）C、2’（x2+y2）+4x2f"（x2+y2）D、2xf"（x2+y2）
查看答案
填空题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。
查看答案
填空题设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝____。
查看答案
单选题设z=f（x2+y2），其中f具有二阶导数，则等于（）．A2f’（x2+y2）B4x2f（x2+y2）C2’（x2+y2）+4x2f（x2+y2）D2xf（x2+y2）
查看答案
填空题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。
查看答案
单选题设方程x2＋y2＋z2＝4z确定可微函数z＝z（x，y），则全微分dz等于（　　）。[2014年真题]A（ydx＋xdy）/（2－z）B（xdx＋ydy）/（2－z）C（dx＋dy）/（2＋z）D（dx－dy）/（2－z）
查看答案
单选题设z＝z（x，y）是由方程xz－xy＋ln（xyz）＝0所确定的可微函数，则∂z/∂y等于（　　）。[2013年真题]A－xz/（xz＋1）B－x＋1/2Cz（－xz＋y）/[x（xz＋1）]Dz（xy－1）/[y（xz＋1）]
查看答案
单选题设z＝yφ（x/y），其中φ（u）具有二阶连续导数，则∂2z/（∂x∂y）等于（　　）。[2017年真题]A（1/y）φ″（x/y）B（－x/y2）φ″（x/y）C1Dφ′（x/y）－（x/y）φ″（x/y）
查看答案
单选题设f有二阶偏导数，z＝f（xy），则∂2z/∂x∂y等于（　　）。Ayf″＋f′Bxy2f″Cxyf′f″Df′＋xyf″
查看答案
填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。
查看答案
热门标签