曲面:x2+y2+z2=2z之内及曲面z=x2+y2之外所围成的立体的体积V等于:
曲面:x2+y2+z2=2z之内及曲面z=x2+y2之外所围成的立体的体积V等于:
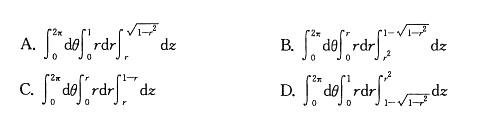
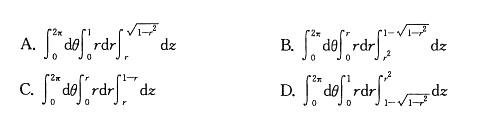
参考解析
解析:

相关考题:
(1)求直线y=1,曲线L以及y轴围成的平面图形绕y轴旋转一周所得到的的旋转体体积A;(2)假定曲线L绕y轴旋转一周所得到的旋转曲面为S。该旋转曲面作为容器盛满水(水的质量密度(单位体积水的重力)等于1),如果将其中的水抽完,求外力作功W.
下列关于曲面方程的结论中,错误的是()。A. 2x2-3y2-z = 1表示双叶双曲面B. 2x2+3y2-z2=1表示单叶双曲面C. 2x2+3y2-z = 1表示椭圆抛物面D. 2(x2+y2)-z2=1 表示锥面
下列关于曲面方程的结论中,错误的是()。A、2x2-3y2-z=1表示双叶双曲面B、2x2+3y2-z2=1表示单叶双曲面C、2x2+3y2-z=1表示椭圆抛物面D、2(x2+y2)-z2=1表示锥面
填空题曲面z=x2+y2与平面2x+4y-z=0平行的切平面的方程是____。