已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1．(Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；(Ⅱ)设求证：数列{cn}是等差数列；(Ⅲ)求数列｛an｝的通项公式及前n项和．
已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1．
(Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；
(Ⅱ)设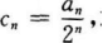
求证：数列{cn}是等差数列；
(Ⅲ)求数列｛an｝的通项公式及前n项和．
(Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；
(Ⅱ)设
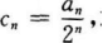求证：数列{cn}是等差数列；
(Ⅲ)求数列｛an｝的通项公式及前n项和．
参考解析
解析：
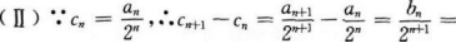
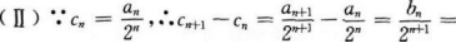
相关考题：
某级数的前两项A1=1，A2=1，以后各项具有如下关系：An=An-2+2An-1下列程序的功能是：要求依次对于整数M=100，1000和10000求出对应的n值，使其满足：Sn＜M且Sn+1≥M，这里Sn=A1+A2+…+An”并依次把n值存入数组单元b[0]，b[l]，b[2]中，请编jsValue()函数来实现此功能，最后调用函数writeDat()把数组b的值输出到out48．dat文件中。注意：部分源程序已给出。请勿改动主函数main()和输出函数writeDat()的内容。试题程序：includeint b[3]；jsValue(){}main(){jsValue( )；printf("M=100，n=%d\nM=1000，n=%d\nM=10000，n=%d\n"，b[0]，b[1]，b[2])；writeDat()；}writeDat ( ){FILE *fp;fp=fopen("out48.dat", "w");fprintf(fp, "%d\n%d\n%d\n",b[0] ,b[1] ,b[2]);fclose (fp);}
级数前n项和Sn=a1+a2+...+an，若an≥0，判断数列﹛Sn﹜有界是级数收敛的什么条件？A.充分条件，但非必要条件B.必要条件，但非充分条件C.充分必要条件D.既非充分条件，又非必要条件
阅读说明和流程图，填补流程图中的空缺（1）?（5），将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1，a2=1，…,an=an-1+an-2!n=3,4,…}的前n项（n>=2) 之和S。例如，菲波那契数列前6项之和为20。计算过程中，当前项之前的两项分别动态地保存在变量A和B中。【流程图】
设数列an的前n项和为Sn，则数列an是等差数列。（1）Sn=n2+2n，n=1，2，3……（2）Sn=n2+2n+1，n=1，2，3……A.条件（1）充分，但条件（2）不充分B.条件（2）充分，但条件（1）不充分C.条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分D.条件（1）充分，条件（2）充分E.条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（ ）A.248B.168C.128D.19E.以上选项均不正确
高中数学《等比数列前n项和》一、考题回顾题目来源：5月19日 上午 重庆市 面试考题试讲题目1.题目：等比数列前n项和2.内容：3.基本要求：(1)引导学生应用等比数列前n项和;(2)试讲10分钟;(3)合理设计板书;(4)要有适当的提问互动环节。答辩题目1.等差数列的前n项和公式是什么?2.怎样才能设计好授课板书呢?你能给出几点建议吗?
已知{an}是由非负整数组成的无穷数列，该数列前n项的最大值记为A。第项之后各(1)若是一个周期为4的数列(即对任意写出dl，dz,d3，d0的值； (2)设d为非负整数，证明：do=一d(n=1，2，3…)的充分必要条件为{an}为公差为d的等差数列： (3)证明：若a1=2，dn=1(n=1，2，3，…)，则{an}的项只能是1或者2，且有无穷多项为l。
单选题已知数列{an}是公差为d的等差数列，Sn是其前n项和，且有S9＜S8＝S7，则下列说法中不正确的是（ ）。AS9＜S10Bd＜0CS7与S8均为Sn的最大值Da8＝0