设平面区域D由曲线y=1/x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
设曲线y=f(x)上任一点(x,y)处的切线斜率为(y/x)+x2,且该曲线经过点(1,1/2)。(1)求函数y=f(x);(2)求由曲线y= f(x),y=O,x=1所围图形绕x轴旋转一周所得旋转体的体积V。
曲线y=x2与y=4—x2所围成的图形的面积为_________.
设随机变量X~t(n)(n>1),则(54)。A.Y~x2(n)B.Y~x2(n-1)C.Y~F(n,1)D.Y~F(1,n)
如果曲线y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( )。A. y=x3-2B. y=2x3-5C. y=x2-2D. y=2x2-5
在区间(0,2π)上,曲线y=sinx与y=cosx之间所围图形的面积是( )。A.B.C.D.
设曲线y=1/x与直线y=x及x=2所围图形的面积为A,则计算A的积分表达式为( ).A.B.C.D.
设方程y-4y+3y=0的某一积分曲线,它在点(0,2)处与直线x-y+2=0相切,则该积分曲线的方程是( ).A.B.C.D.
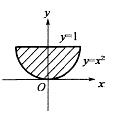
设D是曲线y=x2与y=1所围闭区域,等于:(A)1 (B) (C)0 (D)2
在区间[0,2π]上,曲线:y=sinx与y=cosx之间所围图形的面积是:
设随机变量X和Y都服从N(0,1)分布,则下列叙述中正确的是: A.X+Y~N(0,2) B.X2+Y2~X2分布C. X2和Y2都~X2分布D.X2/Y2~F分布
设D是曲线y=x2 与y=1所围闭区域,A. 1 B.1/2 C. 0 D.2
设L为连接(0,0)点与(1,1)点的抛物线y =x2 ,则对弧长的曲线积分
设 z=f(x2 - y2),则 dz 等于:(A) 2x-2y (B) 2xdx-2ydy (C) f (x2 - y2)dx (D) 2 f(x2 - y2)(xdx- ydy)
设曲线y=^e1?x2与直线x=-1的交点为P,则曲线在点P处的切线方程是( )A.2x-y+2=0B.2x+y+1=0C.2x+y-3=0D.2x-y+3=0
求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.
设区域D={(x,y)(0≤y≤x2,0≤x≤1),则D绕X轴旋转一周所得旋转体的体积为()
设f(x,y)为连续函数,且满足,其中D是由x轴、y轴、所围成的闭区域
设平面闭区域D由x=0,y=0,x+y=1/2,x+y=1 所围成。A.I123B. I132C. I321D. I312
设平面闭区域D={(χ,y)|χ-y+1≥0,χ+y-3≤0,且χ+3y-3≥0}求函数f(χ,y)=3χ-y在D上的最小值,并说明理由。
设D是曲线y=x2与y=1 所围闭区域,等于( )。A. 1 B. 1/2 C.0 D. 2
求由曲线y=x2(x≥0),直线y=1及Y轴围成的平面图形的面积·
设D为曲线y=x2与直线y=x所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.?
设随机变量X和Y都服从N(0,1)分布,则下列叙述中正确的是()。A、X+Y服从正态分布B、X2+Y2~x2分布C、X2和Y2都服从X2分布D、分布
设(X,Y)在由直线y=x,y=2-x,y=0所围的区域内服从均匀分布,则P{0.1
曲线x2=6y-y3在(-2,2)点切线的斜率为()
单选题在竖曲线测设中,关于Y值正确的说法是()。A凹形曲线Y为正;凸形曲线Y为负B凹形曲线Y为正;凸形曲线Y为正C凹形曲线Y为负;凸形曲线Y为负D凹形曲线Y为负;凸形曲线Y为正
多选题设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则y=4X1αX2的均值与方差分别为( )。AE(y)=4BE(y)=20CVar(y)=14DVar(y)=24EVar(y)=15