设曲线y=1/x与直线y=x及x=2所围图形的面积为A,则计算A的积分表达式为( ).A.B.C.D.
设曲线y=1/x与直线y=x及x=2所围图形的面积为A,则计算A的积分表达式为( ).
A.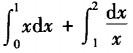
B.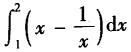
C.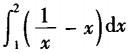
D.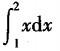
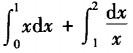
B.
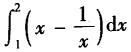
C.
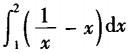
D.
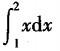
参考解析
解析: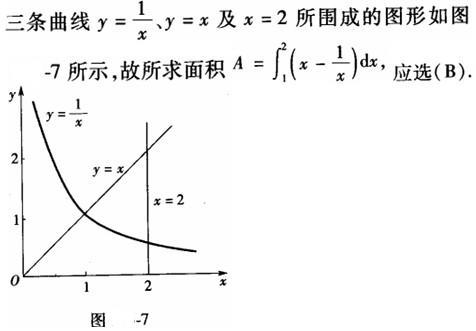

相关考题:
设曲线y=f(x)上任一点(x,y)处的切线斜率为(y/x)+x2,且该曲线经过点(1,1/2)。(1)求函数y=f(x);(2)求由曲线y= f(x),y=O,x=1所围图形绕x轴旋转一周所得旋转体的体积V。
设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是()。A.xyB.x 设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。A.xyB.x<=yC.x‖y+zy-zD.!((x<y)!z‖1)
设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。A.x&&y B.x 设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。A.x&&yB.x<=yC.x||y+z&&y-zD.!((x<y)&&!z||1)
设f(x)、g(x)在区间[a,b]上连续,且g(x)<f(x)<m(m为常数),由曲线y=g(x),y=f(x),x=a及x=b所围平面图形绕直线y=m旋转而成的旋转体体积为( )。A.B.C.D.
单选题由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体体积为:()A(293/60)πBπ/60C4π2D5π