求微分方程满足初始条件的特解
求微分方程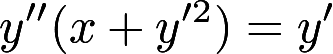 满足初始条件
满足初始条件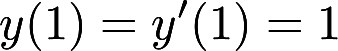 的特解
的特解
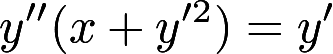 满足初始条件
满足初始条件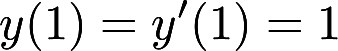 的特解
的特解参考解析
解析:

相关考题:
关于利用积分变换分析电路,下列说法正确的是()。 A、把时域微分方程转换为频域代数方程;再作反变换,可求得满足电路初始条件的原微分方程的解答,不需要确定积分常数。B、把时域微分方程转换为频域低阶微分方程;再作反变换,可求得满足电路初始条件的原微分方程的解答。C、把时域微分方程转换为频域代数方程;再作反变换,可求得满足电路初始条件的原微分方程的解答,需要确定积分常数。D、把时域微分方程转换为频域代数方程,求解频域代数方程即可求得满足电路初始条件的原微分方程的解答。
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=的特解是:(A)cosy=(1+ex) (B)cosy=(1+ex) (C)cosy=4(1+ex) (D)cos2y=(1+ex)
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=π/3的特解是:A. cosy=(1/4) (1+ex) B. cosy=1+exC. cosy=4(1+ex) D. cos2y=1+ex
单选题微分方程cosydx+(1+e-x)sinydy=0满足初始条件y|x=0=π/3的特解是( )。Acosy=(1+ex)/4Bcosy=1+exCcosy=4(1+ex)Dcos2y=1+ex
填空题微分方程y′=ex+y满足条件y(0)=0的特解为____。