设A为m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r1,矩阵B=AC的秩为r,则
下列结论中正确的是( )。A、 矩阵A的行秩与列秩可以不等B、 秩为r的矩阵中,所有r阶子式均不为零C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零D、 秩为r的矩阵中,不存在等于零的r-1阶子式
设A是三阶矩阵,且|A|=4,则=_______.
设A=,B为三阶非零矩阵,且AB=O,则r(A)=_______.
设A1,A2分别为m阶,n阶可逆矩阵,分块矩阵.证明:A可逆,且
设n阶矩阵A满足(aE-A)(bE-A)=O且a≠6.证明:A可对角化.
设A为m阶实对称矩阵且正定,B为m×n实矩阵,B^T为B的转置矩阵,试证:B^TAB为正定矩阵的充分必要条件是B的秩r(B)=n,
设n阶实对称矩阵A的秩为r,且满足,求 ①二次型的标准形; ②行列式的值,其中E为单位矩阵
设A为n阶非零矩阵,且存在自然数k,使得A^k=O.证明:A不可以对角化.
若矩阵A=,B是三阶非零矩阵,满足AB=O,则t=_______.
设A为n阶非奇异矩阵,α为n维列向量,b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
设A、B、C为同阶矩阵,且C为非奇异矩阵,满足,求证:
设A,B为三阶矩阵,且满足方程.若矩阵,求矩阵B.
设A为m×n阶实矩阵,且r(A)=n.证明:A^TA的特征值全大于零.
设A=,且存在三阶非零矩阵B,使得AB=O,则a=_______,b=_______.
设A为三阶实对称矩阵,A的秩为2,且 (Ⅰ)求A的所有特征值与特征向量; (Ⅱ)求矩阵A.
设A为3阶实对称矩阵,A的秩为2,且. (Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A
设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;
问答题设A是n阶矩阵,且满足Am=E,其中m为整数,E为n阶单位矩阵。令将A中的元素aij换成它的代数余子式Aij而成的矩阵为A(~),证明:(A(~))m=E。
问答题设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;
填空题设,B为三阶非零矩阵,且AB=0,则t=____。
单选题设A是m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r,矩阵B=AC的秩为r1,则( )。Ar>r1Br<rlCr=rlDr与r1的关系依C而定
单选题下列结论中正确的是( )A矩阵A的行秩与列秩可以不等B秩为r的矩阵中,所有r阶子式均不为零C若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零D秩为r的矩阵中,不存在等于零的r-1阶子式
 是4阶非零矩阵, 且满足
是4阶非零矩阵, 且满足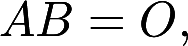 证明矩阵B的秩
证明矩阵B的秩 是4阶非零矩阵, 且满足
是4阶非零矩阵, 且满足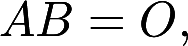 证明矩阵B的秩
证明矩阵B的秩
