设P=,Q为三阶非零矩阵,且PQ=O,则().A.当t=6时,r(Q)=1B.当t=6时,r(Q)=2C.当t≠6时,r(Q)=1D.当t≠6时,r(Q)=2
设A为m×n阶矩阵,B为n×m阶矩阵,且m>n,令r(AB)=r,则().A.r>mB.r=mC.rD.r≥m
设A,B都是,n阶矩阵,其中B是非零矩阵,且AB=O,则().A.r(B)=nB.r(B)C.A2-Bz=(A+B)(A-B)D.｜A｜=0
设A,B皆为n阶矩阵,则下列结论正确的是().A.AB=O的充分必要条件是A=O或B-OB.AB≠O的充分必要条件是A≠0且B≠0C.AB=O且r(A)=N,则B=OD.若AB≠0,则｜A｜≠0或｜B｜≠0
设A是m×n矩阵，B是n×m矩阵，且AB=E,其中E为m阶单位矩阵，则（ ）A.r(A)=r(B)=mB.r(A)=m r(B)=nC.r(A)=n r(B)=mD.r(A)=r(B)=n
设A为四阶非零矩阵,且r(A^*)=1,则().A.r(A)=1B.r(A)=2C.r(A)=3D.r(A)=4
设A、B均为n阶非零矩阵，且AB=0，则R（A），R（B）满足：A.必有一个等于0B.都小于nC. 一个小于n，一个等于nD.都等于n
设A、B均为n阶非零矩阵，且AB=0，则R(A)，R(B)满足：A.必有一个等于0 B.都小于nC. 一个小于n，一个等于n D.都等于n
设A是三阶矩阵,且｜A｜=4,则=_______.
设A是4×3阶矩阵且r(A)=2,B=,则r(AB)=_______.
设A为三阶矩阵,A的第一行元素为a,b,c且不全为零,又B=且AB=0,求方程组AX=0的通解.
设A为n阶非零矩阵,且存在自然数k,使得A^k=O.证明：A不可以对角化.
设A为三阶矩阵,且｜A｜=4,则=_______.
若矩阵A=,B是三阶非零矩阵,满足AB=O,则t=_______.
设A=图},B≠0为三阶矩阵,且BA=0,则r(B)=_______.{
设，B为三阶非零矩阵，且AB=0，则t=________.
设A是4×3矩阵，且r(A)=2，而，则r(AB)=_________.
设A是三阶实对称矩阵,r(A)=1,A^2－3A=O,设（1,1,-1）t为A的非零特征值对应的特征向量.(1)求A的特征值；(2)求矩阵A.
设A,B分别为m×n及n×s阶矩阵,且AB=O.证明：r(A)+r(B)≤n,
设A=,且存在三阶非零矩阵B,使得AB=O,则a=_______,b=_______.
设B≠O为三阶矩阵,且矩阵B的每个列向量为方程组的解,则k=_______,｜B｜=_______.
设A=(aij)是三阶非零矩阵，｜A｜为A的行列式，Aij为aij的代数余子式，若aij+Aij=0(i，j=1，2，3)，则｜A｜=________.
设A，B为三阶矩阵且A不可逆，又AB+2B=O 且r（B）=2，则 |A+4E|=A.8B.16C.2D.0
设 都是n(n≥3）阶非零矩阵，且AB=O，则r（B）=（ ）A. 0B.1C. 2D. 3
填空题设，B为三阶非零矩阵，且AB＝0，则t＝____。
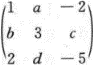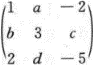,B为三阶非零矩阵,且AB=O,则r(A)=_______.