设，B为三阶非零矩阵，且AB=0，则t=________.

设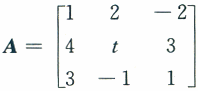，B为三阶非零矩阵，且AB=0，则t=________.

参考解析

解析：由AB=0，对B按列分块有AB=A(β1，β2，β3)=(Aβ1，Aβ2，Aβ3)=(0,0,0)，即β1，β2，β3是齐次方程组Ax=0的解，又因B≠0，故Ax=0有非零解，那么若熟悉公式：AB=0，则r(A)+r(B)≤n.可知r(A)<3.亦可求出t=-3.
【评注】对于AB=O要有B的每个列向量都是齐次方程组Ax=0的构思，还要有秩r(A)+r(B)≤n的知识.

相关考题：

设A,B都是n阶非零矩阵,且AB=0,则A,B的秩____。 A.必有一个等于0B.都小于nC.一个小于n,一个等于nD.都等于n
查看答案
设A、B、C均为n阶矩阵,则下列结论或等式成立的是()。 A、(AB)^2=A^2B^2B、若AB=AC且A≠0，则B=CC、((A+B)C)^T=C^T(B^T+A^T)D、若A≠0且B≠0,则AB≠0
查看答案
设A、B都是n阶非零矩阵，且AB=0，则A和B的秩A.必有一个等于零B.都小于nC.一个小于n，一个等于nD.都等于n
查看答案
设P=,Q为三阶非零矩阵,且PQ=O,则().A.当t=6时,r(Q)=1B.当t=6时,r(Q)=2C.当t≠6时,r(Q)=1D.当t≠6时,r(Q)=2
查看答案
设，B是三阶非零矩阵，且，则（）.
查看答案
已知，P为三阶非零矩阵，且，则
查看答案
设A,B都是,n阶矩阵,其中B是非零矩阵,且AB=O,则().A.r(B)=nB.r(B)C.A2-Bz=(A+B)(A-B)D.｜A｜=0
查看答案
设B是三阶非零矩阵，已知B的每一列都是方程组 的解，则t等于A.0 B.2 C.1 D.-1
查看答案
设A是三阶矩阵,且｜A｜=4,则=_______.
查看答案
设A=,B为三阶非零矩阵,且AB=O,则r(A)=_______.
查看答案
设A为三阶矩阵,A的第一行元素为a,b,c且不全为零,又B=且AB=0,求方程组AX=0的通解.
查看答案
设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值,　　对应特征向量为(-1,0,1)^T.　　(1)求A的其他特征值与特征向量；　　(2)求A.
查看答案
设A为三阶矩阵,且｜A｜=4,则=_______.
查看答案
若矩阵A=,B是三阶非零矩阵,满足AB=O,则t=_______.
查看答案
设A=图},B≠0为三阶矩阵,且BA=0,则r(B)=_______.{
查看答案
设A=,且存在三阶非零矩阵B,使得AB=O,则a=_______,b=_______.
查看答案
设A=(aij)是三阶非零矩阵，｜A｜为A的行列式，Aij为aij的代数余子式，若aij+Aij=0(i，j=1，2，3)，则｜A｜=________.
查看答案
设A，B为三阶矩阵且A不可逆，又AB+2B=O 且r（B）=2，则 |A+4E|=A.8B.16C.2D.0
查看答案
设 都是n(n≥3）阶非零矩阵，且AB=O，则r（B）=（ ）A. 0B.1C. 2D. 3
查看答案
设B是三阶非零矩阵，已知B的每一列都是方程组的解，则t等于A.0B.2C.1D.-1
查看答案
设A，B均为n阶非零矩阵，且AB=0，则RA，RB满足（）。A、必有一个等于0B、都小于nC、一个小于n，一个等于nD、都等于n
查看答案
填空题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝____。
查看答案
填空题设，B为三阶非零矩阵，且AB＝0，则t＝____。
查看答案
单选题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝（　　）。A－2B－1C0D1
查看答案
单选题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝（　　）。A4B2C－1D1
查看答案
单选题设A，B均为n阶非零矩阵，且AB=0，则RA，RB满足（）。A必有一个等于0B都小于nC一个小于n，一个等于nD都等于n
查看答案
单选题设A，B都是n阶非零矩阵，且AB＝0，则A和B的秩（　　）。A必有一个等于零B都等于nC一个小于n，一个等于nD都小于n
查看答案
热门标签