设(X,Y)服从在区域D上的均匀分布,其中D为x轴、y轴及x+y=1所围成,求X与Y的协方差Cov(X,Y).
设函数y=y(x)由方程y+arcsinx=ex+y确定。求dy.
设随机变量与的联合分布律为(1)求X与Y的边缘分布列(2)X与Y是否独立?
设函数f(x,y)=X2+Y2+xy+3,求f(x,y)的极值点与极值.
设X~U(0,2),y=X^2,求y的概率密度函数.
设随机变量X,Y相互独立,且X~N,Y~N,Z=|X-Y|,求 E(Z),D(Z).
设(X,Y)的联合密度函数为f(x,y)= (1)求a;(2)求X,Y的边缘密度,并判断其独立性;(3)求.
设随机变量(X,Y)的联合密度函数为f(x,y)=(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
设随机变量X~N(μ,σ^2),Y~U[-π,π],X,Y相互独立,令Z=X+Y,求fz(z).
设随机变量X~U(0,1),在X=x(0 (1)求X,y的联合密度函数; (2)求y的边缘密度函数.
设X,Y相互独立,且X~B,Y~N(0,1),令U=max{X,Y},求P{1
设随机变量X~E(λ),令Y=,求P(X+Y=0)及FFY(y).
设二维随机变量(X,Y)的联合密度为f(x,y)= (1)求c;(2)求X,Y的边缘密度,问X,y是否独立? (3)求Z=max(X,Y)的密度.
已知矩阵A=与B=相似. (Ⅰ)求x,y; (Ⅱ)求可逆矩阵P使得P^-1AP=B.
设二维离散型随机变量(X,Y)的概率分布为 (Ⅰ)求P{X=2Y); (Ⅱ)求Cov(X-Y,Y).
设随机变量X与Y的概率分布分别为, 且P{X^2=Y^2}=1. (Ⅰ)求二维随机变量(X,Y)的概率分布; (Ⅱ)求Z=XY的概率分布; (Ⅲ)求X与Y的相关系数ρXY.
设函数y(x)是微分方程满足条件y(0)=0的特解. (Ⅰ)求y(x); (Ⅱ)求曲线y=y(x)的凹凸区间及拐点.
设随机变量X与Y相互独立,X的概率分布为P{X=1}=P{X=-1}=,Y服从参数为λ的泊松分布.令Z=XY. (Ⅰ)求Cov(X,Z); (Ⅱ)求Z的概率分布.
设Y=y((x)满足2y+sin(x+y)=0,求y′.
设字长为8位,X=10100101,Y=11000011,求X∧Y, X∨Y ,X Y的结果。
问答题设字长为8位,X=10100101,Y=11000011,求X∧Y, X∨Y ,X Y的结果。
问答题 设X与Y相互独立,X的概率密度为 Y的概率密度为 求:(1)E(2X-3Y+1),D(2X-3Y+1); (2)Cov(X,Y),ρXY.
 与
与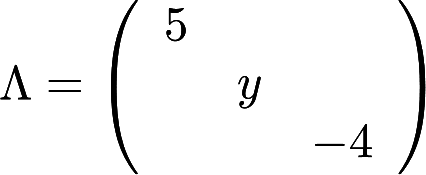 相似, 求x , y
相似, 求x , y 与
与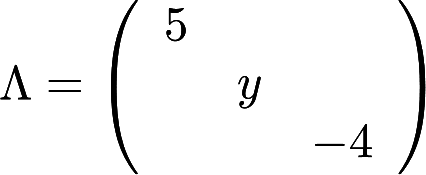 相似, 求x , y
相似, 求x , y

 与
与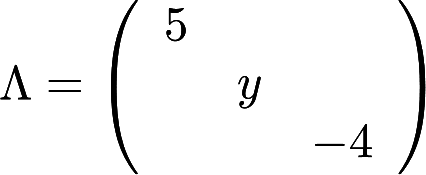 相似, 求x , y
相似, 求x , y