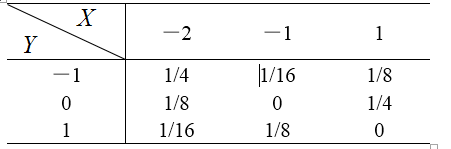
与相互独立,其概率分布分别为求(1)X与Y的联合分布(2)P(X+Y=1)(3)P(X+Y≠1)
设二维随机变量(X,Y)的联合密度函数为f(x,y)= (1)求随机变量X,Y的边缘密度函数; (2)判断随机变量X,Y是否相互独立; (3)求随机变量Z=X+2Y的分布函数和密度函数.
设二维随机变量(X,Y)服从二维正态分布,且X~N(1,3^2),Y~N(0,4^2),且X,Y的相 关系数为-,又设Z=(1)求E(Z),D(Z);(2)求;(3)X,Z是否相互独立?为什么?
设二维随机变量(X,Y)的联合分布律为 则在Y=1的条件下求随机变量X的条件概率分布.
设随机变量X与Y相互独立,下表列出二维随机变量(X,Y)的联合分布律及关于X和Y的边缘分布律的部分数值,试将其余的数值填入表中空白处.
随机变量X与Y相互独立,X服从参数为1的指数分布,Y的概率分布为令Z=XY。X与Z是否相互独立
设随机变量(X,Y)的联合密度为f(x,y)=求: (1)X,Y的边缘密度;(2)P
设X,y的概率分布为X~,Y~,且P(XY=0)=1. (1)求(X,Y)的联合分布;(2)X,Y是否独立?
设随机变量X与Y独立,其中X的概率分布为而Y的概率密度为f(y),求随机变量U=X+Y的概率密度g(u).
设随机变量X,Y相互独立,且X~N(0,4),Y的分布律为Y~.则P(X-1-2Y≤4)=_______.
设随机变量X的分布律为X~,则y=X……2+2的分布律为_______.
设随机变量(X,Y)在区域D={(z,y)|0≤x≤2,0≤y≤1}上服从均匀分布,令 U=,V=. (1)求(U,V)的联合分布;(2)求.
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3. 设随机变量U=max{X,Y},V=min{X,Y}. (1)求二维随机变量(U,V)的联合分布;(2)求Z=UV的分布; (3)判断U,V是否相互独立?(4)求P(U=V).
设随机变量X和Y相互独立,下表列出了二维随机变量(X,Y)的联合分布律及关于X和关于Y的边缘分布律中的部分数值.试将其余数值填入表中的空白处.
设二维随机变量(X,Y)的联合密度为f(x,y)= (1)求c;(2)求X,Y的边缘密度,问X,y是否独立? (3)求Z=max(X,Y)的密度.
随机变量X与Y相互独立,X服从参数为1的指数分布,Y的概率分布为。求Z的概率密度
设随机变量X的概率分布为P{X=1}=P{X=2}=,在给定X=i的条件下,随机变量Y服从均匀分布U(0,i)(i=1,2). (Ⅰ)求Y的分布函数FY(y); (Ⅱ)求EY.
设随机变量X与Y的概率分布分别为, 且P{X^2=Y^2}=1. (Ⅰ)求二维随机变量(X,Y)的概率分布; (Ⅱ)求Z=XY的概率分布; (Ⅲ)求X与Y的相关系数ρXY.
设随机变量X与Y相互独立,X服从参数为1的指数分布,Y的概率分布为P{Y=-1}=p,P{Y=1)=1-p,(0 (Ⅰ)求Z的概率密度; (Ⅱ)p为何值时,X与Z不相关; (Ⅲ)X与Z是否相互独立?
设随机变量X与Y相互独立,X的概率分布为P{X=1}=P{X=-1}=,Y服从参数为λ的泊松分布.令Z=XY. (Ⅰ)求Cov(X,Z); (Ⅱ)求Z的概率分布.
设二维随机变量(X,Y)在区域上服从均匀分布,令 (Ⅰ)写出(X,Y)的概率密度; (Ⅱ)请问U与X是否相互独立?并说明理由; (Ⅲ)求Z=U+X的分布函数F(z).
设随机变量X,Y相互独立,且X的概率分布为P{X=0)=P{X=2)=,Y的概率密度为 (Ⅰ)求P{Y≤EY}; (Ⅱ)求Z=X+Y的概率密度.
设随机变量X,Y相互独立,且X~N,Y~N,则与Z=Y-X同分布的随机变量是().A.X-YB.X+YC.X-2YD.Y-2X
设随机变量X与Y相互独立且都服从区间[0,1]上的均匀分布,则下列随机变量中服从均匀分布的有()。A、X2B、X+YC、(X,Y)D、X-Y
如果随机变量X和Y服从联合正态分布,且X与Y的协方差为0,则X与Y相互独立。
问答题设随机变景X与Y相互独立,且X服从[0,1]上的均匀分布,y服从λ=1的指数分布, 求:(1)X与Y的联合分布函数. (2)X与y的联合概率密度函数. (3)P{X≥Y}.
问答题 随机变量(X,Y)在矩形区域D={(x,y)|a 求:(1)联合概率密度f(x,y). (2)边缘概率密度f X(i),f Y(y). (3)X与Y是否独立?