设(X,Y)的联合密度函数为f(x,y)= (1)求a;(2)求X,Y的边缘密度,并判断其独立性;(3)求.
设(X,Y)的联合密度函数为f(x,y)=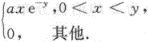
(1)求a;(2)求X,Y的边缘密度,并判断其独立性;(3)求.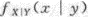
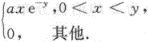
(1)求a;(2)求X,Y的边缘密度,并判断其独立性;(3)求.
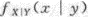
参考解析
解析: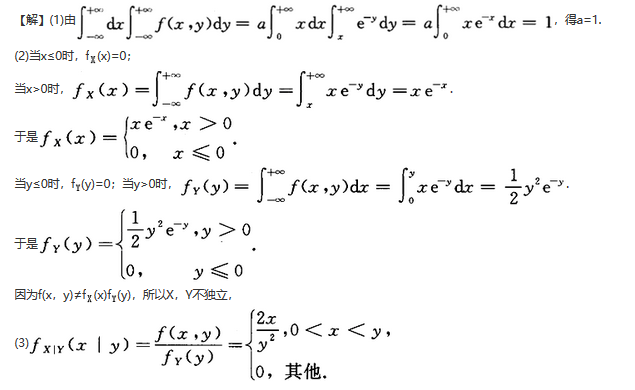
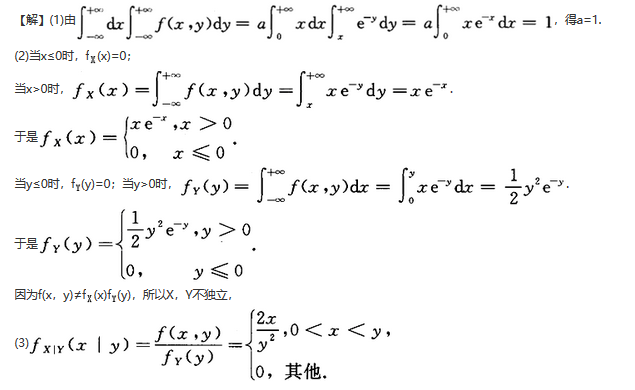
相关考题:
设f(x),f'(x)为已知的连续函数,则微分方程y'十f'(x)y=f(x)f'(x)的通解是:A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +cC. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)
设随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=max{X,Y}的分布函数为 A.AF^2(x)B.F(x)F(y)C.1-[1-F(x)]^2D.[1-F(x)][1-F(y)]
单选题设随机变量X的概率密度函数f(x)=1/[π(1+x2)],则Y=3X的概率密度函数为( )。A1/[π(1+y2)]B3/[π(9+y2)]C9/[π(9+y2)]D27/[π(9+y2)]
单选题设随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=max{X,Y}的分布函数为( )。AF2(x)BF(x)F(y)C1-[1-F(x)]2D[1-F(x)][1-F(y)]