设X,Y相互独立,且X～B,Y～N(0,1),令U=max{X,Y},求P{1
设X,Y相互独立,且X～B
,Y～N(0,1),令U=max{X,Y},求P{1
,Y～N(0,1),令U=max{X,Y},求P{1参考解析
解析：【解】P(U≤u)=P(max{X，Y}≤u)=P(X≤u，Y≤u)=P(X≤u)P(Y≤u)，
P(U≤1.96)=P(X≤1.96)P(Y≤1.96)=［P(X=0)+P(X=1)］P(Y≤1.96)
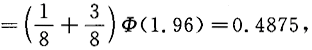
P(U≤1)=P(X≤1)P(Y≤1)=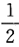
×Ф(1)=0.4205，
则P(1小于U≤1.96)=P(U≤1.96)-P(U≤1)=0.067.
P(U≤1.96)=P(X≤1.96)P(Y≤1.96)=［P(X=0)+P(X=1)］P(Y≤1.96)
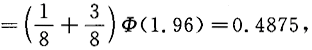
P(U≤1)=P(X≤1)P(Y≤1)=
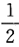×Ф(1)=0.4205，
则P(1小于U≤1.96)=P(U≤1.96)-P(U≤1)=0.067.
相关考题：
设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求： (1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3. 设随机变量U=max{X,Y},V=min{X,Y}. (1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布； (3)判断U,V是否相互独立？(4)求P（U=V）.
单选题设随机变量X与Y相互独立，已知P（X≤1）=p，P（Y≤1）=q，则P（max（X，Y）≤1）等于（）．Ap+qBpqCpDq