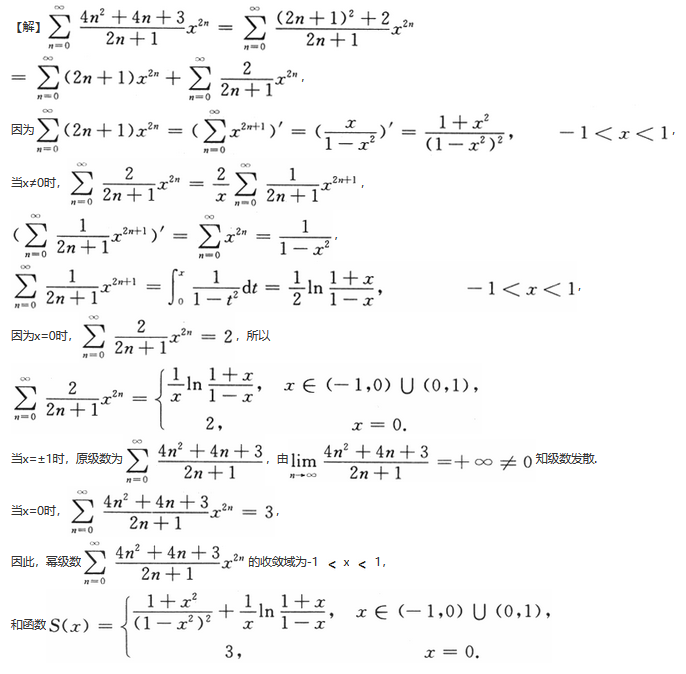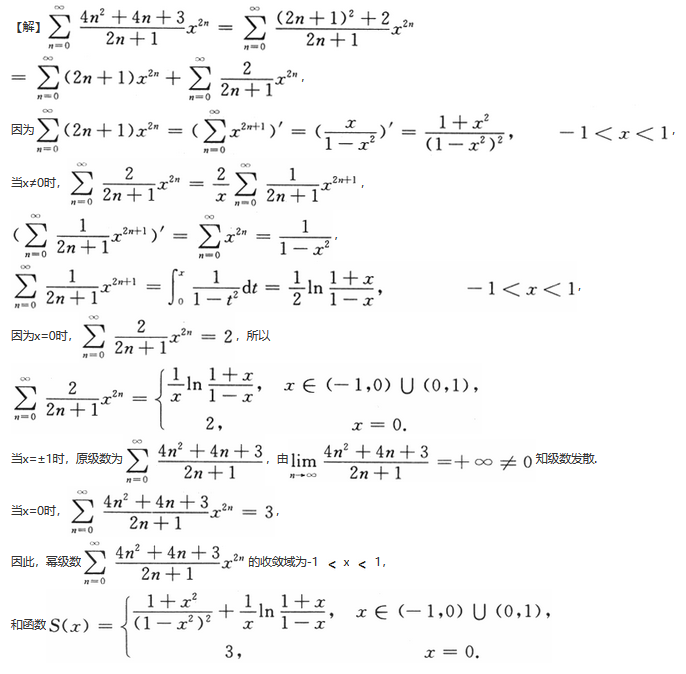将函数f(x)=1/(3-x)展开成(x+1)的幂级数并指出收敛区间(6分)
幂级数的收敛域为( )。A、(-1,1)B、[-1,1]C、[-1,1)D、(-1,1]
幂级数的收敛域是( )。A.[-2,4)B.(-2,4)C.(-1,1)D.
幂级数在区间(-1,1)内的和函数S(x)=________.
设数列{an}满足条件:a0=3,a1=1,,S(x)是幂级数的和函数. (Ⅰ)证明:S"(x)-S(x)=0; (Ⅱ)求S(x)的表达式.
设数列{an}单调减少,无界,则幂级数的收敛域为 A.A(-1,1]B.[-1,1)C.[0,2)D.(0,2]
已知幂级数在x=0处收敛,在x=-4处发散,则幂级数的收敛域为________.
幂级数在(0,+∞)内的和函数S(x)=_________.
幂级数的收敛域为()。A. [-1,1) B. [4,6) C. [4,6] D. (4,6]
设幂级数的收敛半径为2,则幂级数的收敛区间是( )。A. (-2,2) B. (-2,4) C. (0,4) D. (-4,0)
已知幂级数的收敛半径R=1,则幂级数的收敛域为( )。 A. (-1,1] B. [-1,1] C. [-1,1) D.(-∞,+∞)
将f(x)=1/(2-x)展开为x的幂级数,其收敛域为( )。 A. (-1,1) B. (-2,2) C.〔-1/2,1/2) D. (-∞,+∞)
将函数f(x)=xe3x展开为x的幂级数,并指出其收敛区间.
在原点展开的幂级数的收敛域一定是()。A、有界区域B、关于原点对称的区域C、无界区域D、由正数组成的区域
对级数敛散性的判别,幂级数适用于()。A、收敛B、绝对收敛C、绝对一致收敛D、点点收敛
幂级数的收敛半径为2,则幂级数的收敛区间是()A、(-2,2)B、(-2,4)C、(0,4)D、(-4,0)
系统函数H(z)的收敛域如果不包含单位圆(|z|=1),系统不稳定
单选题幂级数的收敛域为()。A[-1,1)B[4,6)C[4,6]D(4,6]
单选题幂级数的收敛半径为2,则幂级数的收敛区间是()A(-2,2)B(-2,4)C(0,4)D(-4,0)
单选题知幂级数的收敛半径R=1,则幂级数的收敛域为()。A(-1,l]B[-1,1]C[-1,1)D(-∞,+∞)
单选题在原点展开的幂级数的收敛域一定是()。A有界区域B关于原点对称的区域C无界区域D由正数组成的区域
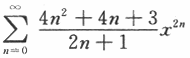 的收敛域及和函数.
的收敛域及和函数.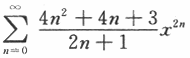 的收敛域及和函数.
的收敛域及和函数.