已知曲线C为y=2x2及直线L为y=4x．①求由曲线C与直线L所围成的平面图形的面积S；②求曲线C的平行于直线L的切线方程．

已知曲线C为y=2x2及直线L为y=4x．
①求由曲线C与直线L所围成的平面图形的面积S；
②求曲线C的平行于直线L的切线方程．

参考解析

解析：画出平面图形如图l一3—4阴影所示．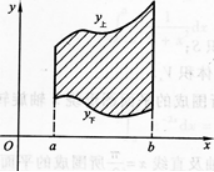
图1—3—3

图1—3—4

相关考题：

已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．
查看答案
设平面区域D由曲线y=1／x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
查看答案
曲线y=xlnx的平行于直线x－y＋1=0的切线方程为()。 A.y=xB.y=-(x+1)C.y=(lnx)(x)D.y=x
查看答案
已知I=50-15i，S=-20+0.1Y，I为投资，S为储蓄，i为银行利率，Y为国民收入，则IS曲线的表达式为()。A:Y=700-150IB:Y=700+150IC:Y=50-150ID:Y=500-150i
查看答案
设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。A.B.C.D.
查看答案
设曲线y=1/x与直线y=x及x=2所围图形的面积为A，则计算A的积分表达式为( ).A.B.C.D.
查看答案
由曲线y=ex，y=e-2x及直线x=-1所围成图形的面积是：
查看答案
已知曲线L的参数方程是，则曲线L上t=π/2处的切线方程是：A. x+y=π B.x-y=π-4 C. x-y=π D.x+y=π-4
查看答案
曲线冬y=1/2x2，x2+y2=8所围成图形的面积(上半平面部分)是:
查看答案
曲线y=2x2在点(1，2)处的切线方程y=______．
查看答案
曲线y=lnx上与直线垂直的切线方程为
查看答案
已知曲线L的方程为y=1-｜x｜(x∈［-1，1］)，起点是(-1，0)，终点为(1，0)，则曲线积分________.
查看答案
曲线y=x2+1与直线y=2x的交点坐标为()
查看答案
χ2+χy+y2=l表示的曲线是( )。A、椭圆B、双曲线C、抛物线D、两条相交直线
查看答案
求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积·
查看答案
已知曲线y=ex与直线y=c(c>1)及Y轴所围成的平面图形的面积为1，求实数c的值。
查看答案
设竖曲线半径为R，长度为L，则竖曲线中点处的纵距y为（）。A、y=L2/2RB、y=L2/8RC、y=2L2/RD、y=8L2/R
查看答案
一平面简谐波沿x轴正向传播，已知x=L（Lλ）处质点的振动方程为y=Acosωt，波速为u，则波动方程为（）A、y=Acosω［t-（x-L）／u]B、y=Acosω［t-（x+L）／u]C、y=Acosω［t+（x+L）／u]D、y=Acosω［t+（x-L）／u]
查看答案
已知直线的斜率为0.5，起点为（X10.，Y10.），终点的X坐标为X50.，则终点的Y坐标为（）。A、Y25.B、Y27.5C、Y28.D、Y30.
查看答案
G01为（），其格式为（）。A、快速点定位，G01X_Y_Z_F_B、直线插补，G01X_Y_Z_F_C、直线插补，G01a_b_y_F_D、曲线插补，G01a_b_y_f_
查看答案
已知直线经过（x1，y1）点，斜率为k(k≠0)，则直线方程为y=2kx+2。
查看答案
一平面简谐波沿X轴正向传播，已知x=L（Lλ）处质点的振动方程为y=Acosωt，波速为u，那么x=0处质点的振动方程为（）。A、y=Acosω（t+L/u）B、y=Acosω（t-L/u）C、y=Acos（ωt+L/u）D、y=Acos（ωt-L/u）
查看答案
已知直线经过（x1，y1）点，斜率为k（k≠0），则直线方程为（）。A、y-y1=k（x-x1）B、y=5kx+3C、y=9k（x-x1）D、y=4x+b
查看答案
单选题在竖曲线测设中，关于Y值正确的说法是（）。A凹形曲线Y为正；凸形曲线Y为负B凹形曲线Y为正；凸形曲线Y为正C凹形曲线Y为负；凸形曲线Y为负D凹形曲线Y为负；凸形曲线Y为正
查看答案
填空题曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为____。
查看答案
单选题曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（　　）。Ay＝exsin2xBy＝－exsin2xCy＝exsinxDy＝－exsinx
查看答案
单选题悬臂梁长度为l，取自由端为坐标原点，则求梁的挠曲线时确定积分常数的边界条件为（）。Ax=0、y=0；x=0、y¢=0Bx=l、y=0；x=l、y¢=0Cx=0、y=0；x=l、y¢=0Dx=l、y=0；x=0、y¢=0
查看答案
热门标签