曲线y=1-x2与x轴所围成的平面图形的面积S=()·A.2B.4/3C.1D.2/3

曲线y=1-x2与x轴所围成的平面图形的面积S=()·

A.2
B.4/3
C.1
D.2/3

参考解析

解析：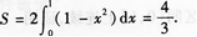

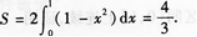
相关考题：

已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．
查看答案
曲线y=x2与y=4—x2所围成的图形的面积为_________．
查看答案
求由曲线y=ex，y=e-x及x=1所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积Vx.
查看答案
曲线y=sinx在[-π，π]上与x轴所围成的图形的面积为( )。A.2B.0C.4D.6
查看答案
过坐标原点作曲线y=lnx的切线，该切线与曲线y=lnx及x轴围成平面图形D。D的面积A和D绕直线x=e旋转一周所得旋转体的体积V分别为（　　）。
查看答案
曲线冬y=1/2x2，x2+y2=8所围成图形的面积(上半平面部分)是:
查看答案
求曲线y=，直线z=1和z轴所围成的有界平面图形的面积s，及该平面图形绕2轴旋转一周所得旋转体的体积V．
查看答案
求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积．
查看答案
设曲线y=4-x2(x≥0)与x轴，y轴及直线x=4所围成的平面图形为D(如图1—3—2中阴影部分所示)．图1—3—1图1—3—2①求D的面积S；②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy．
查看答案
已知曲线C为y=2x2及直线L为y=4x．①求由曲线C与直线L所围成的平面图形的面积S；②求曲线C的平行于直线L的切线方程．
查看答案
已知函数(x)=-x2+2x．①求曲线y=(x)与x轴所围成的平面图形面积S；②求①的平面图形绕x轴旋转一周所得旋转体体积Vx．
查看答案
①求由曲线y=x，y=1/x，x=2与y=0所围成的平面图形的面积S；②求①中的平面图形绕x轴旋转一周所得旋转体的体积V．
查看答案
①求曲线y=x2(x≥0)，y=1与x=0所围成的平面图形的面积S：②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy．
查看答案
在抛物线y=1-x2与x轴所围成的平面区域内作一内接矩形ABCD，其一边AB在x轴上(如图1-2-4所示)．设AB=2x，矩形面积为S(x)．图1—2—3图1—2—4①写出S(x)的表达式；②求S(x)的最大值．
查看答案
设D为曲线y=1-x2，直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·①求平面图形的面积；②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．
查看答案
①求曲线y=ex及直线x=1，x=0，y=0所围成的图形D的面积S：②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．
查看答案
求曲线y=x2与直线y=0，x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积．
查看答案
①求在区间(0，π)上的曲线y=sinx与x轴所围成图形的面积S；②求①中的平面图形绕x轴旋转一周所得旋转体的体积Vx．
查看答案
已知曲线的方程为 ，则曲线 与x 轴围成的平面图形的面积为
查看答案
曲线y=sinx在[-π,π]上与x轴所围成的图形的面积为（ ）。A. 2 B. 0 C. 4 D. 6
查看答案
设抛物线Y=1-x2与x轴的交点为A、B，在抛物线与x轴所围成的平面区域内，以线段AB为下底作内接等腰梯形ABCD(如图2—1所示)．设梯形上底CD长为2x，面积为S(x)．(1)写出S(x)的表达式；(2)求S(x)的最大值．
查看答案
设曲线及x=0所围成的平面图形为D．(1)求平面图形D的面积s．(2)求平面图形D绕y轴旋转一周生成的旋转体体积V
查看答案
求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积·
查看答案
设l是曲线y=x2+3在点(1，4)处的切线，求由该曲线，切线l及Y轴围成的平面图形的面积S．
查看答案
(1)求曲线Y=ex及直线x=1，x=0,y=0所围成的平面图形(如图3—3所示)的面积A．(2)求(1)中平面图形绕x轴旋转一周所得旋转体的体积Vx.
查看答案
已知曲线y=ex与直线y=c(c>1)及Y轴所围成的平面图形的面积为1，求实数c的值。
查看答案
曲线y=sinx在［-π，π]上与x轴所围成的图形的面积为（）。A、2B、0C、4D、6
查看答案
热门标签