设抛物线Y=1-x2与x轴的交点为A、B,在抛物线与x轴所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图2—1所示).设梯形上底CD长为2x,面积为S(x).(1)写出S(x)的表达式;(2)求S(x)的最大值.
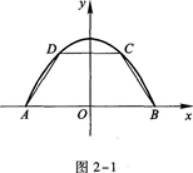
设抛物线Y=1-x2与x轴的交点为A、B,在抛物线与x轴所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图2—1所示).设梯形上底CD长为2x,面积为
S(x).
(1)写出S(x)的表达式;
(2)求S(x)的最大值.
S(x).
(1)写出S(x)的表达式;
(2)求S(x)的最大值.

参考解析
解析:


【评析】求函数fx)在[a,b]上的最值时,如果求出fx)的驻点,一定要先判定驻点是否落在[a,b]上.



【评析】求函数fx)在[a,b]上的最值时,如果求出fx)的驻点,一定要先判定驻点是否落在[a,b]上.
相关考题:
设抛物线y=1-x2与x轴的交点为A,B,在它们所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图1—2-2所示).设梯形上底CD长为2x,面积为S(x).图1一2—1图1—2—2①写出S(x)的表达式;②求S(x)的最大值.
设曲线y=4-x2(x≥0)与x轴,y轴及直线x=4所围成的平面图形为D(如图1—3—2中阴影部分所示).图1—3—1图1—3—2①求D的面积S;②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy.
在抛物线y=1-x2与x轴所围成的平面区域内作一内接矩形ABCD,其一边AB在x轴上(如图1-2-4所示).设AB=2x,矩形面积为S(x).图1—2—3图1—2—4①写出S(x)的表达式;②求S(x)的最大值.
如图。在直角梯形ABCD中,AB∥CD,∠BAD=90o,且AB=8,AD=3,CD=4,动点P,Q分别以点B和点A为起点同时出发,点P沿B→A,以每秒1个单位速度运动,终点为点A;点Q沿A→D→C→B,以每秒1.5个单位速度运动,终点为点B。设△APQ的面积为y,运动时间为x。 (1)求y关于x的函数解析式y=f(x); (2)画出函数y=f(x)的图象。
如图所示,已知A,B为直线L:y=mx-m+2与抛物线y=x2的两个交点。 (1)直线ι经过一个定点C,试求出点C的坐标;(2分) (2)若m=-1,已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合),且△ABP的面积为(3√13)/2,求点P的坐标。(6分)
如,等腰梯形的上底与腰均为x,下底为x+10.则x=13.(1)该梯形的上底与下底之比为13:23.(2)该梯形的面积为216.A.条件(1)充分,但条件(2)不充分。B.条件(2)充分,但条件(1)不充分。C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分。D.条件(1)充分,条件(2)也充分。E.条件(1)和(2)单独都不充分,条件(1)和(2)联合起来也不充分。
单选题垂直于x轴的动直线与过原点的曲线y=y(x)(x≥0,y≥0)以及x轴围成一个以[0,x]为底边的曲边梯形,其面积为y3(x).函数y(x)的隐函数形式是().Ay2-x=0By2+x=0C3y2-2x=0D2y-3x2=0