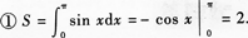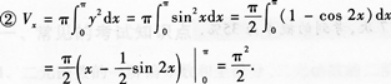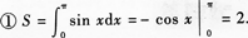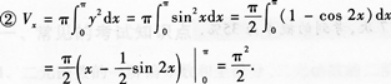求由曲线y=ex,y=e-x及x=1所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积Vx.
求曲线y=2-x2和直线y=2x+2所围成图形面积.
在区间(0,2π)上,曲线y=sinx与y=cosx之间所围图形的面积是( )。A.B.C.D.
曲线y=sinx在[-π,π]上与x轴所围成的图形的面积为( )。A.2B.0C.4D.6
在区间[0,2π]上,曲线:y=sinx与y=cosx之间所围图形的面积是:
求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.
设曲线y=4-x2(x≥0)与x轴,y轴及直线x=4所围成的平面图形为D(如图1—3—2中阴影部分所示).图1—3—1图1—3—2①求D的面积S;②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy.
已知曲线C为y=2x2及直线L为y=4x.①求由曲线C与直线L所围成的平面图形的面积S;②求曲线C的平行于直线L的切线方程.
已知函数(x)=-x2+2x.①求曲线y=(x)与x轴所围成的平面图形面积S;②求①的平面图形绕x轴旋转一周所得旋转体体积Vx.
①求由曲线y=x,y=1/x,x=2与y=0所围成的平面图形的面积S;②求①中的平面图形绕x轴旋转一周所得旋转体的体积V.
①求曲线y=x2(x≥0),y=1与x=0所围成的平面图形的面积S:②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy.
求曲线y=x2,与该曲线在x=a(a>o)处的切线与x轴所围的平面图形的面积.
①求曲线y=ex及直线x=1,x=0,y=0所围成的图形D的面积S:②求平面图形D绕x轴旋转一周所成旋转体的体积Vx.
曲线y=1-x2与x轴所围成的平面图形的面积S=()·A.2B.4/3C.1D.2/3
求曲线y=x2与直线y=0,x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积.
曲线Y=x2,x=0,x=2,Y=0所围成的图形的面积为( ).
设f(x)为区间[a,b]上的连续函数,则曲线y=f(x)与直线x=a,x=b,y=0所围成的封闭图形的面积为( ).《》( )
曲线y=sinx(0≤x≤π/2)与直线x=π/2,y=0围成的平面图形绕x轴旋转产生的旋转体体积是()。
曲线y=sinx在[-π,π]上与x轴所围成的图形的面积为( )。A. 2 B. 0 C. 4 D. 6
设曲线及x=0所围成的平面图形为D.(1)求平面图形D的面积s.(2)求平面图形D绕y轴旋转一周生成的旋转体体积V
求由曲线y=x2(x≥0),直线y=1及Y轴围成的平面图形的面积·
设l是曲线y=x2+3在点(1,4)处的切线,求由该曲线,切线l及Y轴围成的平面图形的面积S.
(1)求曲线Y=ex及直线x=1,x=0,y=0所围成的平面图形(如图3—3所示)的面积A.(2)求(1)中平面图形绕x轴旋转一周所得旋转体的体积Vx.
曲线y=cosx在[0,2π]上与x轴所围成图形的面积是:()A、0B、4C、2D、1
曲线y=sinx在[-π,π]上与x轴所围成的图形的面积为()。A、2B、0C、4D、6
单选题曲线y=cosx在[0,2π]上与x轴所围成图形的面积是:()A0B4C2D1
单选题曲线y-=cosx在[0,2π]上与x轴所围成图形的面积是:()A0B4C2D1