微分方程y''=(y')2的通解是:A. lnx+c B. ln(x+c)C. c2+ln x+c1 D. c2-lnlx+c1 (以上各式中,c1、c2为任意常数)
微分方程y''=(y')2的通解是:
A. lnx+c B. ln(x+c)
C. c2+ln x+c1 D. c2-lnlx+c1
(以上各式中,c1、c2为任意常数)
A. lnx+c B. ln(x+c)
C. c2+ln x+c1 D. c2-lnlx+c1
(以上各式中,c1、c2为任意常数)
参考解析
解析:提示:此题为可降阶的高阶微分方程,按方程不显含变量y计算。
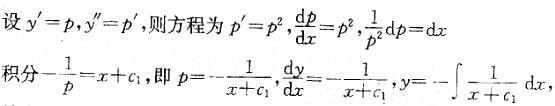
y=c2-lnlx+c1
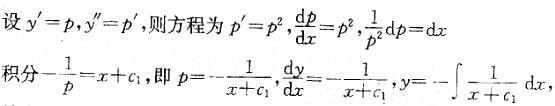
y=c2-lnlx+c1
相关考题:
已知微分方程y'+p(x)y = q(x)[q(x)≠0]有两个不同的特解y1(x), y2(x),C为任意常数,则该微分方程的通解是:A.y=C(y1-y2)B. y=C(y1+y2)C. y=y1+C(y1+y2)D. y=y1+C(y1-y2)
单选题(2012)已知微分方程y′+p+(x)y=q(x)[q(x)≠0]有两个不同的特解y1(x),y2(x),则该微分方程的通解是:(c为任意常数)()Ay=c(y1-y2)By=c(y1+y2)Cy=y1+c(y1+y2)Dy=y1+c(y1-y2)
填空题微分方程x2y″+3xy′-3y=x3的通解为____。