微分方程y′-y=0的通解为().A.y=ex+CB.y=e-x+CC.y=CexD.y=Ce-x
微分方程y′-y=0的通解为().
A.y=ex+C
B.y=e-x+C
C.y=Cex
D.y=Ce-x
B.y=e-x+C
C.y=Cex
D.y=Ce-x
参考解析
解析:所给方程为可分离变量方程.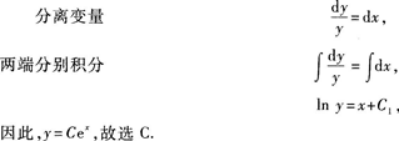
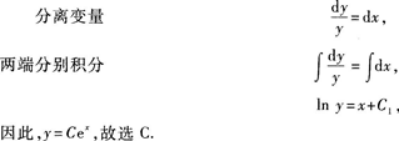
相关考题:
在下列微分方程中,以函数y=C1e^-x+C2e^4x(C1,C2为任意常数)为通解的微分方程是( )。A. y″+3y′-4y=0 B. y″-3y′-4y=0 C. y″+3y′+4y=0 D. y″+y′-4y=0
填空题微分方程xy″+3y′=0的通解为____。