若D是由x=0,y=0,x2+y2=1所围成在第一象限的区域,则二重积分等于( )。
若D是由x=0,y=0,x2+y2=1所围成在第一象限的区域,则二重积分

等于( )。

等于( )。
参考解析
解析:采用极坐标法求二重积分,具体计算如下:
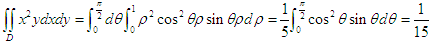
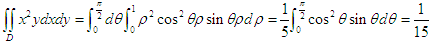
相关考题:
已知某直线的坐标方位角为210°15′,则可知直线( )。A.位于第一象限,△X、△Y大于0B.位于第二象限,△X小于0、△Y大于0C.位于第三象限,△X、△Y小于0D.位于第四象限,△X大于0、△Y小于0
单选题以下关于二元函数的连续性的说法正确是( )。A若f(x,y)沿任意直线y=kx在点x=0处连续,则f(x,y)在(0,0)点连续B若f(x,y)在点(x0,y0)点连续,则f(x0,y)在y0点连续,f(x,y0)在x0点连续C若f(x,y)在点(x0,y0)点处偏导数fx′(x0,y0)及fy′(x0,y0)存在,则f(x,y)在(x0,y0)处连续D以上说法都不对
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A1B-1C1/7D-1/7
单选题设f(x,y)与φ(x,y)均为可微函数,且φy′(x,y)≠0。已知(x0,y0)是f(x,y)在约束条件φ(x,y)=0下的一个极值点,下列选项正确的是( )。A若fx′(x0,y0)=0,则fy′(x0,y0)=0B若fx′(x0,y0)=0,则fy′(x0,y0)≠0C若fx′(x0,y0)≠0,则fy′(x0,y0)=0D若fx′(x0,y0)≠0,则fy′(x0,y0)≠0
单选题I=∮L(-ydx+xdy)/(x2+y2),因为∂Q/∂x=∂P/∂y=(y2-x2)/(x2+y2)2,所以( )。A对任意闭曲线L,I=0B在L为不含原点在内的闭区域的边界线时I=0C因为∂Q/∂x=∂P/∂y在原点不存在,故对任意L,I≠0D在L含原点在内时I=0,不含原点时I≠0