已知D为x轴、y轴和抛物线y=1-x2所围成的在第一象限内的闭区域,则
已知D为x轴、y轴和抛物线y=1-x2所围成的在第一象限内的闭区域,则
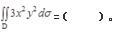
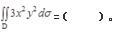
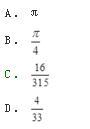
参考解析
解析:积分区域D形状如图所示。

计算得抛物线与x轴、y轴的交点分别为(1,0)、(0,1),从而D={(x,y)|0≤y≤1-x2,x∈[0,1]},则


计算得抛物线与x轴、y轴的交点分别为(1,0)、(0,1),从而D={(x,y)|0≤y≤1-x2,x∈[0,1]},则

相关考题:
单元体的应力状态如图所示,其σ1的方向:A.在第一、三象限内,且与x轴成小于45°的夹角B.在第一、三象限内,且与y轴成小于45°的夹角C.在第二、四象限内,且与x轴成小于45°的夹角D.在第二、四象限内,且与y轴成小于45°的夹角
设抛物线y=1-x2与x轴的交点为A,B,在它们所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图1—2-2所示).设梯形上底CD长为2x,面积为S(x).图1一2—1图1—2—2①写出S(x)的表达式;②求S(x)的最大值.
在抛物线y=1-x2与x轴所围成的平面区域内作一内接矩形ABCD,其一边AB在x轴上(如图1-2-4所示).设AB=2x,矩形面积为S(x).图1—2—3图1—2—4①写出S(x)的表达式;②求S(x)的最大值.
设抛物线Y=1-x2与x轴的交点为A、B,在抛物线与x轴所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图2—1所示).设梯形上底CD长为2x,面积为S(x).(1)写出S(x)的表达式;(2)求S(x)的最大值.
测量使用的高斯平面直角坐标系与数学使用的笛卡儿坐标系的区别是()。A、x与y轴互换,第一象限相同,象限逆时针编号B、x与y轴互换,第一象限相同,象限顺时针编号C、x与y轴不变,第一象限相同,象限顺时针编号D、x与y轴互换,第一象限不同,象限顺时针编号
测量使用的高斯平面直角坐标系与数学使用的笛卡尔坐标系的区别是()。A、x与y轴互换,第一象限相同,象限逆时针编号B、x与y轴互换,第一象限相同,象限顺时针编号C、x与y轴不变,第一象限相同,象限顺时针编号D、x与y轴互换,第一象限不同,象限顺时针编号
单选题第一象限内曲线y2+6x=36和坐标轴所围成的图形绕x轴旋转所生成的旋转体的体积为().A36πB54πC72πD108π