矩阵的特征值为( )。A、λ1=λ2=1,λ3=2B、λ1=1,λ2=λ3=2C、λ1=1,λ2=2,λ3=3D、λ1=λ2=1,λ3=3
矩阵
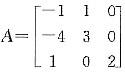 的特征值为( )。
的特征值为( )。
A、λ1=λ2=1,λ3=2
B、λ1=1,λ2=λ3=2
C、λ1=1,λ2=2,λ3=3
D、λ1=λ2=1,λ3=3
B、λ1=1,λ2=λ3=2
C、λ1=1,λ2=2,λ3=3
D、λ1=λ2=1,λ3=3
参考解析
解析:A的特征多项式 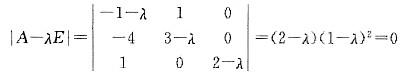 特征值为λ1=λ2=1,λ3=2
特征值为λ1=λ2=1,λ3=2
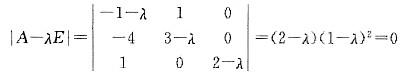 特征值为λ1=λ2=1,λ3=2
特征值为λ1=λ2=1,λ3=2
相关考题:
设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆B.矩阵A的迹为零C.特征值-1,1对应的特征向量正交D.方程组AX=0的基础解系含有一个线性无关的解向量
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。A、α是矩阵-2A的属于特征值-2λ的特征向量B、α是矩阵的属于特征值的特征向量C、α是矩阵A*的属于特征值的特征向量D、α是矩阵AT的属于特征值λ的特征向量
单选题设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。Aα是矩阵-2A的属于特征值-2λ的特征向量Bα是矩阵的属于特征值的特征向量Cα是矩阵A*的属于特征值的特征向量Dα是矩阵AT的属于特征值λ的特征向量
单选题已知n阶可逆矩阵A的特征值为λ0,则矩阵(2A)-1的特征值是( )。[2012年真题]A2/λ0Bλ0/2C1/(2λ0)D2λ0