山西省曲沃中学校2016届高三数学上学期10月阶段性考试试题文

已知“a=[1,2,3]”且“b=a[:]”,则执行“a[1]=10”后,b的值为()。

A.[10,2,3]

B.[1,10,3]

C.[1,2,10]

D.[1,2,3]


参考答案：D

已知“a[1,[2,3]]”且“ba[]”,则执行“a[1][0]10”后,b的值为。()

A、[1,10]

B、[1,[2,3]]

C、[1,[10,3]]

D、报错


正确答案:C

已知函数y=f（x）是奇函数，且f（-5）=3，则f（5）= （ ）

A.5

B.3

C.-3

D.-5


正确答案：C
本题主要考查的知识点为奇函数的性质．【应试指导】由于f(z)是奇函数，故f(5)=f(-5)=-3．

已知集合A={x|x≤1},B={x|≥a},且A∪B=R，

则实数a的取值范围是__________________.


正确答案：
 2.ɑ≤1 

已知函数在x0处可导，则f ’(x0)的值是：
A. 4 B. -4 C.-2 D. 2


答案：C
解析：
提示:用导数定义计算。

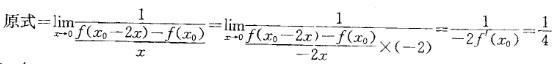
故f'(x0) = -2

高三年级数学测试题二（文） 一、选择题（每题5分，共60分）1、已知集合,则集合等于（ ）A. B. C. D. 2、已知命题，则为（ ）A， B，C， D，3、已知函数f（x）为奇函数，且当x0时，则f（1）=（）A 2 B 0 C 1 D 24、已知为第二象限角,且,则的值是( )A B. C. D.5、已知, 则下列不等式一定成立的是（ ）A B C D6、已知向量，若向量的夹角为，则实数（ ）A2 B C0 D7、已知等差数列中，（ ）A B C30 D158、已知为第二象限角，则（ ）A、 B、 C、 D、9、如果实数、满足条件 则的最大值为（ ）A B C D 10、如果函数的图象经过第一、二、四象限，不经过第三象限，那么一定有（ ）A BC D 11、曲线y2x33x1在点（1，0）处的切线方程为（ ）Ay4x5 By3x2Cy4x4 Dy3x312、设是平行四边形的对角线的交点，为四边形所在平面内任意一点，则（ ）（A） （B）（C） （D）二、填空题（每题5分，共20分）13、函数的定义域为 14、若复数，则|z|=15、若正数满足，则的最小值是_16、如图是函数在一个周期内的图象，则其解析式是 三、解答题（共70分）17、（10分）曲线yxln x在点（e，e）处的切线与直线xay1垂直，求实数a的值。18、（12分）在平面直角坐标系中，A、B两点的坐标分别为（1，2），（3，8），向量=（x，3）（1）若，求x的值；（2）若，求x的值19、（12分）在中，内角、的对边分别是、，且（1）求；（2）若，求20、（12分）已知函数（1）求函数f（x）的极值（2）求函数在上的最大值和最小值21、（12分）已知函数，（1）求函数的单调递增区间；（2）求函数在区间上的最大值和最小值22、（12分）已知数列是首项为，公比的等比数列，数列满足（1）求证：是等差数列；（2）求数列的前项和参考答案（文数）一、单项选择B D A D C B D D D B D D二、填空题 5 三、解答题17、218、（1），（2）（），（），19、（1）；（2）20、（1）极大值为f（-1）=2，极小值为f（1）=-2（2）最大值和最小值分别为2，18.（1）f（x）=3x2-3=3（x+1）（x-1）令f（x）=0得x1=1，x2=1列表如下：x（-，1）1（1，1）1（1，+）f（x）+00+f（x）增极大值减极小值增f（x）的极大值为f（-1）=2，极小值为f（1）=-2（2）由（1）可知，在上的最值只可能在x=-3，x=，x=-1.x=1取到，f（-3）=18，f（-1）=2，f（1）=2，f（）=在上的最大值和最小值分别为2，18.21、（1）（2）最大值，最小值（1）由，解得所以函数单调递增区间为（2）当时，所以当即时，函数取得最大值，当即时，函数取得最小值22、（1）由题意，数列是首项为1，公差为3的等差数列（2）由（1）知，两式相减得，- 5 -

已知(x)在区间(-∞，+∞)内为单调减函数，且(x)>(1)，则x的取值范围是()．

A.(-∞，-l)
B.(-∞，1)
C.(1，+∞)
D.(-∞，+∞)

答案：B
解析：
利用单调减函数的定义可知：当(x)>(1)时，必有x<1．

已知集合A={1，m}，B={2，3}，A ∩B={2}，则A∪B=_____。


答案：
解析：
{1，2，3}。解析：因为A∩B={2}，所以m=2，A={1，2}，A∪B={1，2，3}。

已知集合A={x|x2-3x-4>0}，集合B={x|m+1≤x≤4m}，若B?A，则实数m的取值范围为()。

A.(-∞，3)
B.(-(1/4)，3)
C.(-∞，-(1/4))∪(3，+∞)
D.(-∞，1/3)∪(3，+∞)

答案：D
解析：

已知 a2+a+1=0，则 a2008+a2009+1的值为（）。

A.0
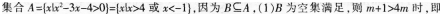
B.1
C.2
D.3

答案：A
解析：
由a2+a+1=0，联想到逆用立方差公式，求出a3的值，进而通过转化求代数式的值。
如果 a=1，那么 a2+a+1=1+1+1=3≠0，即 a≠1。
等式两边同乘以a-1，得到(a-1)(a2+a+1)=a3-1=0，即a3=1。

因为2007能整除3，所以a2007=1。
a2008+a2009+1=a2007(a2+a)+1=a2+a+1=0。

已知函数y=f（x）是奇函数，且f（-2）=-6，则f（2）= （　　）

A.-2
B.6
C.2
D.-6

答案：B
解析：

相关考题：

考题 已知函数y=f（x）是奇函数，且f（-2）=-6，则f（2）= （　　）A.-2 B.6 C.2 D.-6 答案：B解析：
查看答案
考题 若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则的值为()。A. 0 B. 1 C. 2 D.不存在答案：B解析：提示：利用积分上限函数求导和洛必达法则。
查看答案
考题 填空题已知集合A＝{a2，d＋1，－3}，B＝{a－3，2a－1，a2＋11，若A∩B＝{－3}，则实数a的值为____．正确答案： -1解析： ∵A∩B＝{－3}，∴－3∈B∵ a2＋1＞0∴集合B中元素有a－3＝－3，或2a－1＝－3．当a－3＝－3，即a＝0时，A＝{0，1，－3}，B＝{－3，－1，1}，得A∩B＝{1，－3}，与已知A∩B＝{－3}相矛盾，故舍去a＝0；当2a－1＝－3，即a＝－1时，A＝1，0，－3}，B＝{－4，－3，2}，A∩B＝{－3}符合题意．∴a＝－1
查看答案
考题 已知集合A={x∣x2-3x-4>0}，集合B={x∣m+1≤x≤4m)，若B∈A，则实数m的取值范围为( )。答案：D解析：
查看答案
考题 若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则的值为()。A. 0 B. 1 C. 2 D.不存在答案：B解析：提示：利用积分上限函数求导和洛必达法则。
查看答案
考题 已知集合A={-2，1，2}，B={x|x2-x-2=0}，则A∩B=( )。A.ψB.{2}C.{1}D.{-2}答案：B解析：因为B={x∣x2-x-2=0}={-1，2}，所以A∩B={2}。
查看答案
考题 已知矩阵,则A的秩r(A)等于（ ）。A. 0 B. 1 C. 2 D. 3答案：C解析：提示： A = 0，但A中有二阶子式不为零，r(A)=2,应选C。
查看答案
考题 已知(x)是偶函数且满足(x+3)=(x)，(1)=-1，则(5)+(11)等于( )A.-2B.2C.-1D.1答案：A解析：【考情点拨】本题主要考查的知识点为偶函数与 周期函数的性质．【应试指导】∵(x)是偶函数，∴(-x)=(x)，
查看答案
考题 填空题已知集合A＝{a2，d＋1，－3}，B＝{a－3，2a－1，a2＋11，若A∩B＝{－3}，则实数a的值为____．正确答案： -1解析： ∵A∩B＝{－3}，∴－3∈B∵ a2＋1＞0∴集合B中元素有a－3＝－3，或2a－1＝－3．当a－3＝－3，即a＝0时，A＝{0，1，－3}，B＝{－3，－1，1}，得A∩B＝{1，－3}，与已知A∩B＝{－3}相矛盾，故舍去a＝0；当2a－1＝－3，即a＝－1时，A＝1，0，－3}，B＝{－4，－3，2}，A∩B＝{－3}符合题意．∴a＝－1
查看答案
考题 若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则的值为()。A. 0 B. 1 C. 2 D.不存在答案：B解析：提示：利用积分上限函数求导和洛必达法则。
查看答案
热门标签
最新考题
最新试卷
热门试卷