若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则的值为()。A. 0 B. 1 C. 2 D.不存在
若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则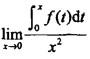
的值为()。
A. 0 B. 1 C. 2 D.不存在
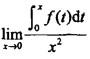的值为()。
A. 0 B. 1 C. 2 D.不存在
参考解析
解析：提示：利用积分上限函数求导和洛必达法则。
相关考题：
以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
已知函数f(x,y)在点(0,0)的某个邻域内连续，且 ，则A.点(0,0)不是f(x,y)的极值B.点(0,0)是f(x,y)的极大值点C.点(0,0)是f(x,y)的极小值点D.根据所给条件无法判断点(0,0)是否为f(x,y)的极值点
设函数f(x)在x=a的某个邻域内连续，且f(a)为其极大值，则存在δ＞0，当x∈(a-δ，a+δ)时，必有( )。A.(x-a)[f(x)-f(a)]≥0B.(x-a)[f(x)-f(a)]≤0C.D.
设函数f（x）在点x=a处可导，则函数｜f（x）｜在点x=a处不可导的充分条件是（ ）A.f（a）=0且f′（a）=0B.f（a）=0且f′（a）≠0C.f（a）＞0且f′（a）＞D.f（a）＜0且f′（a）＜
下列命题正确的是（）A.函数f(x)的导数不存在的点，一定不是f(x)的极值点B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0D.若函数f(x)在点x0处连续，则f'(x0)一定存在
(Ⅰ)证明拉格朗日中值定理：若函数f(x)在［a，b］上连续，在(a，b)内可导，则存在ξ∈(a，b)，使得f(b)-f(a)=f'(ξ)(b-a)；(Ⅱ)证明：若函数f(x)在x=0处连续，在(0，δ)(δ>0)内可导，且=A，则存在，且.
下列命题中正确的为（）A.若xo为f(x)的极值点，则必有，f'(xo)=0B.若f'(xo)=0，则点xo必为f(x)的极值点C.若f'(xo)≠0，则点xo必定不为f(x)的极值点D.若f(x)在点xo处可导，且点xo为f(x)的极值点，则必有f'(xo)=0
单选题设函数f（x）满足关系式f″（x）＋[f′（x）]2＝x，且f′（0）＝0，则（ ）。Af（0）是f（x）的极大值Bf（0）是f（x）的极小值C点（0，f（0））是曲线y＝f（x）的拐点Df（0）不是f（x）的极值，点（0，f（0））也不是曲线y＝f（x）的拐点
单选题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（ ）。Af″（x）＋f（x）＝0Bf′（x）＋f（x）＝0Cf″（x）＋f′（x）＝0Df″（x）＋f′（x）＋f（x）＝0
单选题下列说法中正确的是（ ）。[2014年真题]A若f′（x0）=0，则f（x0）必须是f（x）的极值B若f（x0）是f（x）的极值，则f（x）在点x0处可导，且f′（x0）=0C若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的必要条件D若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的充分条件
单选题设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（ ）。Af′（x）＋f（x）＝0Bf′（x）－f（x）＝0Cf″（x）＋f（x）＝0Df″（x）－f（x）＝0