该切线与抛物线及x轴成的平面去区域为D，求该区域分别绕x轴和y轴旋转而成的体积。
该切线与抛物线及x轴成的平面去区域为D，求该区域分别绕x轴和y轴旋转而成的体积。参考解析
解析：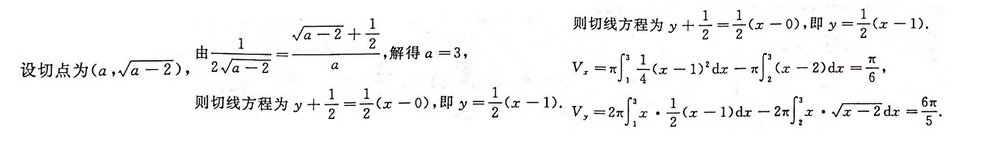
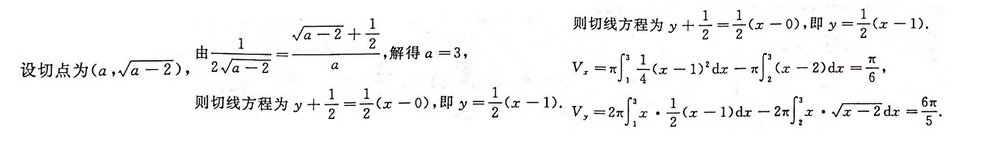
相关考题：
设曲线y=f(x)上任一点(x，y)处的切线斜率为(y/x)+x2，且该曲线经过点（1，1/2）。（1）求函数y=f(x)；（2）求由曲线y= f(x），y=O，x=1所围图形绕x轴旋转一周所得旋转体的体积V。
旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得？A. xOy平面上的双曲线绕x轴旋转所得B. xOz平面上的双曲线绕z轴旋转所得C. xOy平面上的橢圆绕x轴旋转所得 D. xOz平面上的椭圆绕x轴旋转所得
设曲线y=4-x2(x≥0)与x轴，y轴及直线x=4所围成的平面图形为D(如图1—3—2中阴影部分所示)．图1—3—1图1—3—2①求D的面积S；②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy．
旋转曲面x2-y2-z2=1是下列哪个曲线绕何轴旋转所得（）？A、xOy平面上的双曲线绕x轴旋转所得B、xOz平面上的双曲线绕z轴旋转所得C、xOy平面上的椭圆绕x轴旋转所得D、xOz平面上的椭圆绕x轴旋转所得
单选题旋转曲面x2-y2-z2=1是下列哪个曲线绕何轴旋转所得（）？AxOy平面上的双曲线绕x轴旋转所得BxOz平面上的双曲线绕z轴旋转所得CxOy平面上的椭圆绕x轴旋转所得DxOz平面上的椭圆绕x轴旋转所得