设L是从点(0,0)沿:y=1- x-1 至点(2,0)的折线段,则曲线积分xdy等于:A. 0 B. -1 C. 2 D. -2
设L是从点(0,0)沿:y=1- x-1 至点(2,0)的折线段,则曲线积分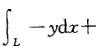 xdy等于:
xdy等于:
A. 0 B. -1 C. 2 D. -2
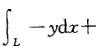 xdy等于:
xdy等于:
A. 0 B. -1 C. 2 D. -2
参考解析
解析: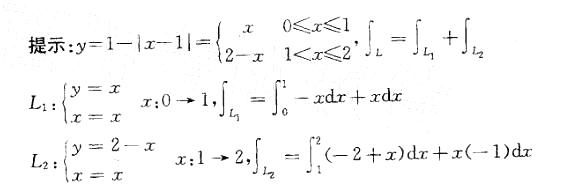
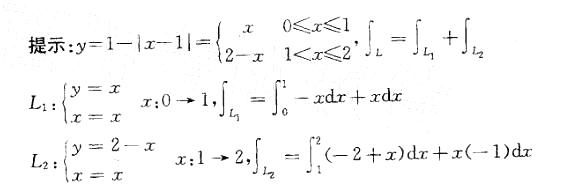
相关考题:
已知函数f(x,y)在点(0,0)的某个邻域内连续,且 ,则A.点(0,0)不是f(x,y)的极值B.点(0,0)是f(x,y)的极大值点C.点(0,0)是f(x,y)的极小值点D.根据所给条件无法判断点(0,0)是否为f(x,y)的极值点
设f(x)=|x(1-x)|,则( ).《》( )A.x=0是f(x)的极值点,但(0,0)不是曲线y=f(x)的拐点B.x=0不是f(x)的极值点,但(0,0)是曲线y=f(x)的拐点C.x=0是f(x)的极值点,且(0,0)是曲线y=f(x)的拐点D.x=0不是f(x)的极值点,(0,0)也不是曲线y=f(x)的拐点
单选题设函数y=f(x)由方程e2x+y-cos(xy)=e-1所确定,则曲线y=f(x)在点(0,1)处的法线方程为( )。Ay+1=x/2By-1=x/2Cy+1=xDy-1=x