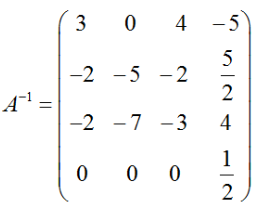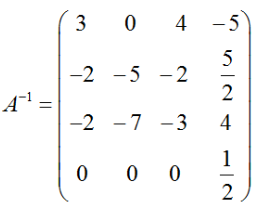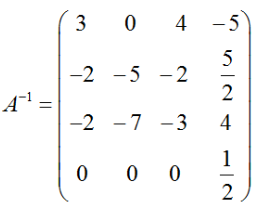matlab中,表示()A.矩阵A的逆右乘BB.B矩阵A的逆左乘BC.矩阵B的逆左乘AD.矩阵B的逆右乘A
设A1,A2分别为m阶,n阶可逆矩阵,分块矩阵.证明:A可逆,且
设,用初等行变换的方法求A的逆矩阵.然后据此将A分解成初等矩阵的乘积.
设矩阵相似于矩阵. (1)求a,b的值;(2)求可逆矩阵P,使为对角阵
设A为n阶非奇异矩阵,α为n维列向量,b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
设A为3×3矩阵,|A|=|-2|.把A按列分块为,其中是A的第j列.求 (1); (2).
设A,B为三阶矩阵,且满足方程.若矩阵,求矩阵B.
设矩阵A= (1)已知A的一个特征值为3,试求y; (2)求可逆矩阵P,使(AP)^T(AP)为对角矩阵.
已知矩阵A=与B=相似. (Ⅰ)求x,y; (Ⅱ)求可逆矩阵P使得P^-1AP=B.
已知a是常数,且矩阵可经初等列变换化为矩阵. (Ⅰ)求a; (Ⅱ)求满足AP=B的可逆矩阵P.
MATLAB中用()函数完成矩阵的求逆运算,用()函数求矩阵的行列式。
设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;
下面()不属于特殊矩阵。A、对角矩阵B、三角矩阵C、稀疏矩阵D、对称矩阵
问答题设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;
填空题MATLAB中用()函数完成矩阵的求逆运算,用()函数求矩阵的行列式。