设A为非奇异对称矩阵,则____仍为对称矩阵。 A.A的转置B.A的逆矩阵C.3AD.A与A的转置的乘积
两个初等矩阵的乘积仍是初等矩阵。() 此题为判断题(对，错)。
用一初等矩阵左乘一矩阵B,等于对B施行相应的()变换。 A、行变换B、列变换C、既不是行变换也不是列变换
Diffie－Hellman的安全性建立在( )。 A、将大数因子分解成素数B、自动机求逆C、无限域上取对数D、求解矩阵
高斯消去法是对增广矩阵(A|b)进行一系列的初等行变换。() 此题为判断题(对，错)。
阐述矩阵乘法的运算过程。并用矩阵乘积形式表示如下线性方程组。 用初等变换的方法求解上述线性方程组。
初等矩阵（ ）A.都可以经过初等变换化为单位矩阵B.所对应的行列式的值都等于1C.相乘仍为初等矩阵D.相加仍为初等矩阵
设a为N阶可逆矩阵，则（ ）.A.若AB=CB，则a=C：B.C.A总可以经过初等变换化为单位矩阵E：D.以上都不对.
设a为N阶可逆矩阵，则（ ）.A.若AB=CB，则a=CB.C.A总可以经过初等变换化为单位矩阵ED.以上都不对
设A为m×n阶矩阵,且r(A)=mAA的任意m个列向量都线性无关BA的任意m阶子式都不等于零C非齐次线性方程组AX=b一定有无穷多个解D矩阵A通过初等行变换一定可以化为
设二次型 (b>0), 其中二次型的矩阵A的特征值之和为1，特征值之积为-12. (1)求a，b的值； (2)利用正交变换将二次型f化为标准形，并写出所用的正交变换和对应的正交矩阵.
设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B. (1)证明B可逆； (2)求AB^-1.
设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B， (1)证明B可逆； (2)求.
已知a是常数，且矩阵可经初等列变换化为矩阵. (Ⅰ)求a； (Ⅱ)求满足AP=B的可逆矩阵P.
设A为m X n矩阵，且r(A)=m小于n，则下列结论正确的是 AA的任意m阶子式都不等于零 BA的任意m个子向量线性无关 C方程组AX=b一定有无数个解 D矩阵A经过初等行变换化为
设二次型的正惯性指数p=2,负惯性指数q=0,且可用可逆线性变换x=Cy将其化为二次型（1）求常数a; (2）求可逆线性变换矩阵C
设 A为 n 阶方阵，B是 A 经过若干次初等行变换得到的矩阵，则下列结论正确的是（ ）。A.|A|=|B|B.|A|≠|B|C.若|A|=0，则一定有 |B|=0D.若 |A|＞ 0，则一定有 |B|＞ 0
设A为n阶方阵，B是A经过若干次矩阵的初等变换后所得到的矩阵，则有（ ）.《》（ ）
设A为4阶魔术矩阵，分别对A进行如下操作： 求矩阵A的逆； 求矩阵A的行列式； 求矩阵A的秩； 求矩阵A的迹；
矩阵的初等行变换不包括的形式有（）。A、将某一行乘上一个不等于零的系数B、将任意两行互换C、将某一行乘上一个不等于零的系数再加到另一行上去D、将某一行加上一个相同的常数
傅立叶变换的实质是将视网膜得到的图像的密度矩阵分解成一定频率上的（）A、图像B、信号C、动作D、声音
问答题设A为4阶魔术矩阵，分别对A进行如下操作： 求矩阵A的逆； 求矩阵A的行列式； 求矩阵A的秩； 求矩阵A的迹；
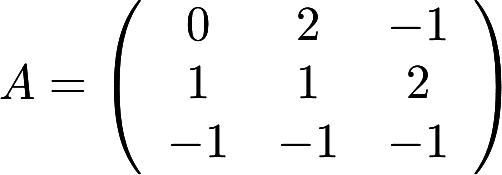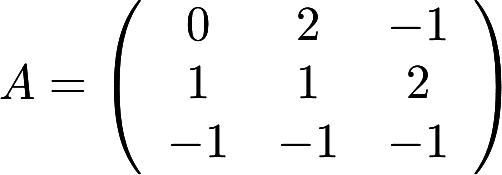，用初等行变换的方法求A的逆矩阵.然后据此将A分解成初等矩阵的乘积.