设A,B均为n阶矩阵,(I一B)可逆,则矩阵方程A＋BX=X的解X=()。
设A,B均为n阶可逆矩阵,求证:(AB)*=B*A*。
设A,B为正定矩阵,C是可逆矩阵,下列矩阵不是正定矩阵的是().
设A,B为n阶矩阵,则下列结论正确的是().A.若A,B可逆,则A+B可逆B.若A,B可逆,则AB可逆C.若A+B可逆,则A-B可逆D.若A+B可逆,则A,B都可逆
设A，B为同阶可逆矩阵，则( )。A.AB=BAB.C.D.存在可逆矩阵P和Q，使PAQ=B
对任一矩阵A，则一定是（ ）.A.可逆矩阵B.不可逆矩阵C.对称矩阵D.反对称矩阵
设N阶矩阵A与对角矩阵合同,则A是().A.可逆矩阵B.实对称矩阵C.正定矩阵D.正交矩阵
已知n阶可逆矩阵A的特征值为λ0，则矩阵(2A)-1的特征值是：
设A1，A2分别为m阶，n阶可逆矩阵，分块矩阵.证明：A可逆，且
试证：如果A,B都是n阶正定矩阵，则A+B也是正定的
设矩阵相似于矩阵. （1）求a,b的值；（2）求可逆矩阵P，使为对角阵
设A，B都是n阶矩阵，AB+E可逆．证明BA+E也可逆，并且．
设n阶矩阵A满足，（1）证明A，A+2E，A+4E可逆，并求它们的逆；（2）当时，判断是否可逆，并说明理由。
设A，B，A+B都是可逆矩阵，证明可逆，并求其逆矩阵.
设P为可逆矩阵,A=P^TP.证明：A是正定矩阵.
设矩阵A= (1)已知A的一个特征值为3，试求y; (2)求可逆矩阵P，使(AP)^T(AP)为对角矩阵.
已知矩阵A=与B=相似. (Ⅰ)求x，y； (Ⅱ)求可逆矩阵P使得P^-1AP=B.
已知a是常数，且矩阵可经初等列变换化为矩阵. (Ⅰ)求a； (Ⅱ)求满足AP=B的可逆矩阵P.
设A为n阶非零矩阵，E为n阶单位矩阵，若A^3=O，则 A.AE-A不可逆，E+A不可逆B.E-A不可逆，E+A可逆C.E-A可逆，E+A可逆D.E-A可逆，E+A不可逆
均为n阶可逆矩阵，则=( )。A．B．A+BC．D．
设A为n阶非零矩阵，E为n阶单位矩阵。若A3=0，则( )。A.E－A不可逆，E+A不可逆B.E—A不可逆。E+A可逆C.E—A可逆。E+A可逆D.E—A可逆。E十A不可逆
设A，B，A+B，A-1+ B-1均为n阶可逆矩阵，则(A-1+ B-1)-1=( )。A、A-1+ B-1B、A+BC、A(A+B) -1 BD、(A+B) -1
设A，N，A+B，A-1+B-1均为n阶可逆矩阵，则（A-1+B-1）=（）。A、A-1+B-1B、A+BC、C.A（A+-1BD、D.（A+-1
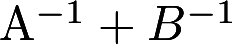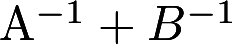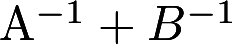也可逆，并求其逆矩阵.