设A^TA=E,证明：A的实特征值的绝对值为1.

设A^TA=E,证明：A的实特征值的绝对值为1.

参考解析

解析：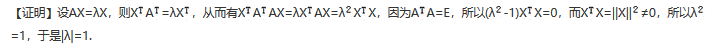

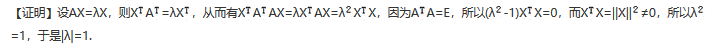
相关考题：

设三阶实对称矩阵的特征值为3,3,0,则A的秩r(A)=() A、2B、3C、4D、5
查看答案
设三阶矩阵A的特征值为1,1,2,则2A＋E的特征值为()。 A、3，5B、1，2C、1，1，2D、3，3，5
查看答案
设A为三阶方阵,其特征值为1,－1,2,则A^2的特征值为1,1,4。() 此题为判断题(对，错)。
查看答案
设A为n阶实对称矩阵,则(). A.A的n个特征向量两两正交B.A的n个特征向量组成单位正交向量组C.A的k重特征值λ0,有r(λ0E-A)=n-kD.A的k重特征值λ。，有r(λ0E-A)=k
查看答案
设A是n阶实对称矩阵，则A有n个()特征值.
查看答案
设是非奇异矩阵A的特征值，则矩阵（2A3）- 1有一个特征值为：A.3B.4C.D.1
查看答案
设A是实对称矩阵，C是实可逆矩阵，.则（ ）.A.A与B相似B.A与B不等价C.A与B有相同的特征值D.A与B合同
查看答案
设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知a是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：A. Pa B. P-1A C. PTa D.（P-1）Ta
查看答案
设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知α是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：(A) Pα (B) P-1α (C) PTa (D) P(-1)Ta
查看答案
设A,B为n阶矩阵.　　(1)是否有AB～BA；(2)若A有特征值1,2,…,n,证明：AB～BA.
查看答案
设3阶实对称矩阵A的特征值为－1，1，1，与特征值－1对应的特征向量x＝（－1，1，1）′，求A
查看答案
设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值,　　对应特征向量为(-1,0,1)^T.　　(1)求A的其他特征值与特征向量；　　(2)求A.
查看答案
设A是n阶正定矩阵,证明:｜E+A｜>1.
查看答案
设实对称阵A的特征值为0，2，2，且对应特征值2的两个特征向量为与，求.
查看答案
设α,β为三维非零列向量,（α,β）=3,A=αβ^T,则A的特征值为_______.
查看答案
设A,B同时发生,则C发生,证明：P(C)≥P(A)+P(B)-1.
查看答案
设A为实对称矩阵,且A的特征值都大于零.证明：A为正定矩阵.
查看答案
设A是m×n阶矩阵,若A^TA=O,证明：A=0.
查看答案
设A是三阶实对称矩阵,r(A)=1,A^2－3A=O,设（1,1,-1）t为A的非零特征值对应的特征向量.(1)求A的特征值；(2)求矩阵A.
查看答案
设f(x)二阶可导，f(0)= f(1),且f(x)在[0,1]上的最小值为—1.证明：
查看答案
设A为m×n阶实矩阵,且r(A)=n.证明：A^TA的特征值全大于零.
查看答案
设A是n阶矩阵,λ是A的特征值,其对应的特征向量为X,证明：λ^2是λ^3的特征值,X为特征向量,若A^2有特征值λ,其对应的特征向量为X,X是否一定为A的特征向量？说明理由.
查看答案
设, 证明A的特征值只能取1或2
查看答案
设A是3阶实对称矩阵,满足，并且r(A)=2. (1) 求A的特征值. (2)当实数k满足什么条件时A+kE正定?
查看答案
设A为三阶实对称矩阵，A的秩为2，且　　(Ⅰ)求A的所有特征值与特征向量；　　(Ⅱ)求矩阵A.
查看答案
设A为三阶实对称矩阵，如果二次曲面方程　　　　在正交变换下的标准方程的图形如图所示，　　　　则A的正特征值的个数为 A.A0B.1C.2D.3
查看答案
设A为3阶实对称矩阵，A的秩为2，且. （Ⅰ）求A的特征值与特征向量； （Ⅱ）求矩阵A
查看答案
热门标签