设A为三阶实对称矩阵,如果二次曲面方程 在正交变换下的标准方程的图形如图所示, 则A的正特征值的个数为 A.A0B.1C.2D.3
设A为三阶实对称矩阵,如果二次曲面方程

在正交变换下的标准方程的图形如图所示,
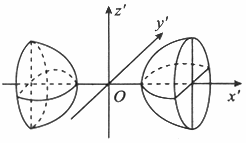
则A的正特征值的个数为

在正交变换下的标准方程的图形如图所示,

则A的正特征值的个数为
A.A0
B.1
C.2
D.3
B.1
C.2
D.3
参考解析
解析:本题把线性代数与解析几何的内容有机的联系起来,首先要明白所给图形是什么曲面?其标准方程是什么? 双叶双曲面,标准方程是: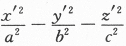 =1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).
=1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).
很多考生选择(C),是不是把标准方程记成了图1} 而忽略了本题的条件是x^TAx=1.
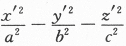 =1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).
=1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).
很多考生选择(C),是不是把标准方程记成了图1} 而忽略了本题的条件是x^TAx=1.
相关考题:
设A,B是正定实对称矩阵,则().A. AB,A+B一定都是正定实对称矩阵B. AB是正定实对称矩阵,A+B不是正定实对称矩阵C. A+B是正定实对称矩阵,AB不一定是正定实对称矩阵D. AB必不是正定实对称矩阵,A+B必是正定实对称矩阵
设A为3阶实对称矩阵,A的秩为2,且. (Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A