解线性方程组其中 .
解线性方程组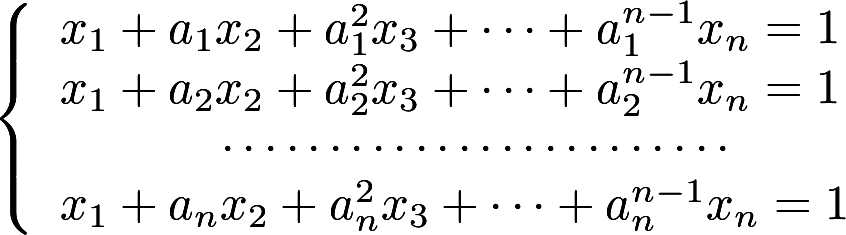 其中
其中 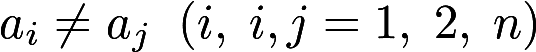 .
.
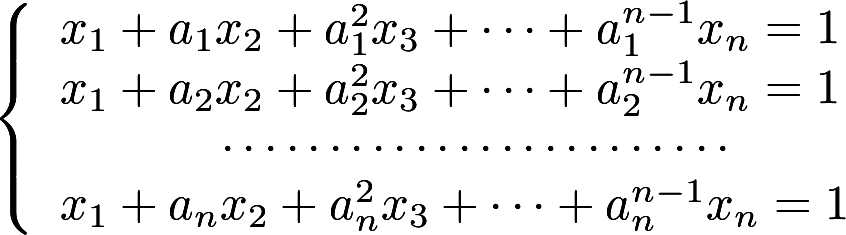 其中
其中 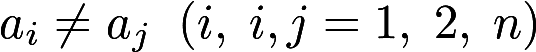 .
.参考解析
解析: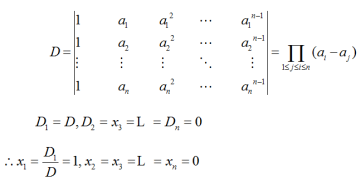
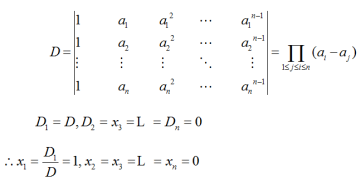
相关考题:
设有齐次线性方程组Ax=0及Bx=0,其中A、B均为m×n矩阵,现有以下4个命题 ①若Ax=0的解均是Bx=0的解,则rA≥rB; ②若rA≥rB,则Ax=0的解均是Bx=0的解; ③若Ax=0与Bx=0同解,则rA=rB; ④若rA=rB,则Ax=0与Bx=0同解。 以上命题中正确的是()。A、①②B、①③C、②④D、③④
设A是4×6矩阵,则齐次线性方程组AX=0解的情况是()。A、无解B、只有零解C、有非零解D、不一定