若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则( )A.A与B相似B.C.A=BD.A与B不一定相似,但|A|=|B|
若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则( )
A.A与B相似
B.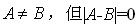
C.A=B
D.A与B不一定相似,但|A|=|B|
A.A与B相似
B.
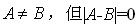
C.A=B
D.A与B不一定相似,但|A|=|B|
参考解析
解析:
相关考题:
设A为m*n矩阵,则有()。 A、若mn,则有ax=b无穷多解B、若mn,则有ax=0非零解,且基础解系含有n-m个线性无关解向量;C、若A有n阶子式不为零,则Ax=b有唯一解;D、若A有n阶子式不为零,则Ax=0仅有零解。
设A为n阶实对称矩阵,则(). A.A的n个特征向量两两正交B.A的n个特征向量组成单位正交向量组C.A的k重特征值λ0,有r(λ0E-A)=n-kD.A的k重特征值λ。,有r(λ0E-A)=k
n*n矩阵可看作是n维空间中的线性变换,矩阵的特征向量经过线性变换后,只是乘以某个常数(特征值),因此,特征向量和特征值在应用中具有重要的作用。下面的矩阵(其中w1、w2、w3均为正整数)有特征向量(w1,w2,w3),其对应的特征值为( )。A.1/3B.1C.3D.9
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。A、α是矩阵-2A的属于特征值-2λ的特征向量B、α是矩阵的属于特征值的特征向量C、α是矩阵A*的属于特征值的特征向量D、α是矩阵AT的属于特征值λ的特征向量
单选题设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。Aα是矩阵-2A的属于特征值-2λ的特征向量Bα是矩阵的属于特征值的特征向量Cα是矩阵A*的属于特征值的特征向量Dα是矩阵AT的属于特征值λ的特征向量
问答题设有三个非零的n阶(n≥3)方阵A1、A2、A3,满足Ai2=Ai(i=1,2,3),且AiAj=0(i≠j,i、j=1,2,3),证明: (1)Ai(i=1,2,3)的特征值有且仅有0和1; (2)Ai的对应于特征值1的特征向量是Aj的对应于特征值0的特征向量(i≠j); (3)若α(→)1、α(→)2、α(→)3分别为A1、A2、A3的对应于特征值1的特征向量,则向量组α(→)1、α(→)2、α(→)3线性无关。