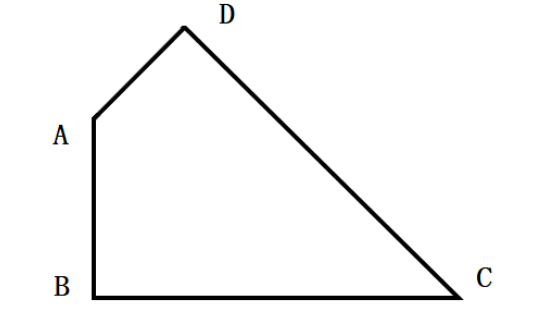
如图,已知一个四边形中边AD长为3cm,边BC长7cm;∠DAB=135°,∠ABC=∠ADC=90°那么这个四边形的面积是( )cm2。
如图,已知一个四边形中边AD长为3cm,边BC长7cm;∠DAB=135°,∠ABC=∠ADC=90°那么这个四边形的面积是( )cm2。
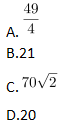

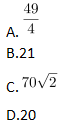
参考解析
解析:第一步,本题考查几何问题,用割补平移法解题。
第二步,作BA和CD的延长线交于E,如图所示,得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB=135°,∠ABC=∠ADC=90°,可以求得∠DCB=360°-135°-90°×2=45°,且∠BEC=∠EAD=45°,所以△EBC和△ADE都是等腰直角三角形。
第三步,因为AD长3cm,BC长7cm,则BE=BC=7cm,DE=AD=3cm,所以
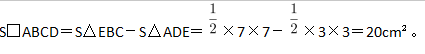
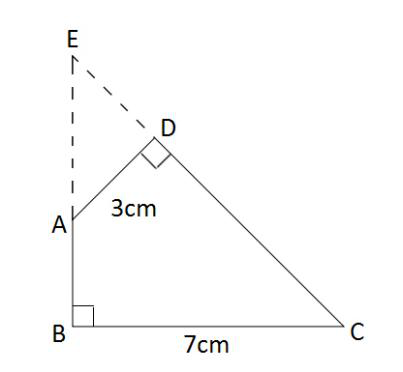
第二步,作BA和CD的延长线交于E,如图所示,得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB=135°,∠ABC=∠ADC=90°,可以求得∠DCB=360°-135°-90°×2=45°,且∠BEC=∠EAD=45°,所以△EBC和△ADE都是等腰直角三角形。
第三步,因为AD长3cm,BC长7cm,则BE=BC=7cm,DE=AD=3cm,所以
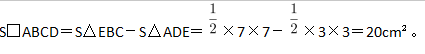

相关考题:
用字母表示:(1)加法结合律:____________________________________________________;(2)乘法结合律:___________________________________________;(3)乘法对加法的分配律:_______________________________________;(4)一个长方形的长为b,宽是长的一半,它的周长是______;面积是______;(5)一个三角形的三边长都为c,它的周长是______;(6)一个平行四边形的一边长为a,该边上的高是其长的2/3 ,这个平行四边形的面积是______。
在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
(1)如果一个菱形绕对角线的交点旋转90°后,所得图形与原来的图形重合,那么这个菱形 是正方形吗?为什么?(2)如果一个四边形绕对角线的交点旋转90°后,所得图形与原来的图形重合,那么这个四边形是正方形吗?为什么?
对边相等,对角相等的凸四边形,是平行四边形吧? 方法①∠B小于90°;左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:过A作AN⊥BC于N;过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法②∠B大于90°左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:延长CD,过A作AN⊥BC于N;延长AB,过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法③∠B等于90°证明:∵∠B=∠D=90°;AB=CD;AC=AC∴△ABC=△ADC(HL)∴AB=CB∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。有错吗?若我的证明有错请明示,我知道有个反例,但它是凹四边形。
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.
如图,平行四边形ABCD的面积是54平方厘米,点E、F、G分别是平行四边形ABCD边上的中点,H为AD边上的任意一点,则阴影部分的面积为( )平方厘米。A. 27B. 28C. 32D. 36
单选题婆罗摩笈多给出的四边形面积公式在只针对()成立。A折四边形B凹四边形C圆内接四边形D圆外切四边形