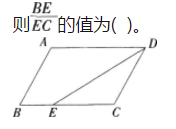
如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E，且AD=14，DC=9，

如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E，且AD=14，DC=9，



参考解析

解析：

相关考题：

如图，BD=CD，AE∶DE=1∶2，延长BE交AC于F，且AF=5cm，则AC的长为( )。A. 30cmB. 25cmC. 15cmD. 10cm
查看答案
平行四边形ABCD的周长是28cm，CD－AD＝2cm，则AB的长度是（ ）。A．8cmB．6cmC．7cmD．9cm
查看答案
设有关系模式R(ABCD),其函数依赖集F={A→B,BC→D },__函数依赖不能被F所逻辑蕴涵 A.AC→DB.B→DC.AD→BD.AC→B
查看答案
在平行四边形ABCD中，∠DAB＝60°，AB＝15cm．已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F，⊙O在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止，试求⊙O滚过的路程．
查看答案
平行四边形中，已知AB、BC及其夹角∠ B（∠ B是锐角），能求出平行四边形ABCD的面积S吗？如果能，写出用AB，BC及其夹角∠ B表示S的式子。
查看答案
如图．已知圆⊙O是△ABC的外接圆，AD是圆⊙0的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB。 (1)求证：BE是⊙0的切线； (2)若BC=√3，AC=5，求圆的直径AD及切线BE的长。
查看答案
(6分)如图，点P为矩形ABCD边BC上一点(不包括端点)，E为BC延长线上一点，CQ为∠DCE的角平分线，连接AP，PQ，使AP⊥PQ。求证：当AB=BC时，存在AP=PQ。
查看答案
在平行四边形ABCD中，∠DAB=60，AB=15cm，已知圆O的半径等于3cm，AB，AD分别与圆O相切于点E，F.圆0在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止．试求圆O滚过的路程．
查看答案
如右图，在直角梯形ABCD中，AB,∥CD，AD⊥CD，AB=1cm，AD=6cm，CD=9cm，则BC=________cm．
查看答案
如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.(1)求证：AB=BC； (2)当BE⊥AD于E时，试证明：BE=AE+CD.
查看答案
如图，边长为a的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________。
查看答案
如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E,且AD=14，DC=9，则BE/EC的值为()。 A.1/3B.4/9C.5/9D.2/3
查看答案
如图所示，△ABC中DE∥BC，且BO和CO分别是∠ABC和∠ACB的角平分线。已知AB=25.4 cm，BC=24.5 cm，AC=20 cm。问△ADE的周长是多少？ A．45.4 cm B．45.1 cm C．44.8 cm D．44.5 cm
查看答案
如图所示，梯形ABCD，AD∥BC，DE⊥BC，现在假设AD、BC的长度都减少10%，DE的长度增加10%，则新梯形的面积与原梯形的面积相比，会怎样变化？ A. 不变B. 减少1%C. 增加10%D. 减少10%
查看答案
如图所示，梯形ABCD的两条对角线AD、BC相交于O，EF平行于两条边且过O点。现已知AB=6，CD=18。问EF的长度为多少？ A. 8.5B. 9C. 9.5D. 10
查看答案
如图6-9所示,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为（ ）A.3B.7.5C.15D.30E.5.5
查看答案
如图7，在四边形ABCD中，AD∥BC，要使四边形ABCD为平行四边形，则应添加的条件是__________（添加一个条件即可）。
查看答案
如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）A、6cm　B、8cmC、10cm　　D、12cm
查看答案
如图，等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8， AB∥DE，求△DEC的周长。
查看答案
如图，平行四边形ABCD的面积是54平方厘米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上的任意一点，则阴影部分的面积为（ ）平方厘米。A. 27B. 28C. 32D. 36
查看答案
如图所示，在△ABC中，AD是∠BAC的平分线，AD = 15，AC=12，CD=9，则点D到AB边的距离是（ ）。A. 12 B. 10C. 9 D.无法确定
查看答案
如图在ΔABC中，DE∥BC，若AD：DB=1：3，DE=2，则BC等于( )。A.8B.6C.4D.2
查看答案
分别用分析法，综合法证明如下命题。 命题：如图：三角形ABC的角B和角C的角平分线相交于点0，过点O作平行于底边BC的直线，交AB边于点D，交AC边于点E，则DE=BD+EC。
查看答案
如图，四棱锥S-ABCD的底面是矩形，SA⊥底面ABCD，P是BC边的中点，AD=2，SA=AB=1。 (1)求证：PD⊥平面SAP； (2)求三棱锥S-APD的体积。
查看答案
已知四棱锥P-ABCD底面为直角梯形，AB平行于DC，∠DAB=90°，PA垂直于底面ABCD，PA=AD=DC=AB=1，M为PB中点。 (1)求证：面PAD⊥面PCD； (2)求面AMC与面BMC所成二面角的余弦值。
查看答案
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90o，E是CD的中点。 (1)证明：CD⊥平面PAE； (2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P-ABCD的体积。
查看答案
如图，已知△ABC的两条角平分线AD和CE相交于H，∠B=60。，F在AC上，且AE=AF．(1)证明：B，D，H，E四点共圆；(2)证明：CE平分∠DEF．
查看答案
热门标签