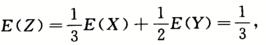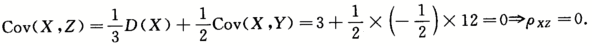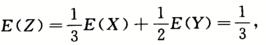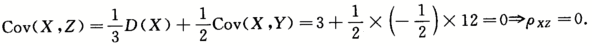两独立随机变量X和Y都服从正态分布,且X~N(3,4),Y~N(2,9)求D(X＋Y)=()。
设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X＋Y服从的分布为() A、X+Y服从N(0，1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布
设随机变量X和Y相互独立,且X~N(2,42),Y~N(3,92),则D(X＋Y)=()
设随机变量和是相互独立的随机变量且都服从正态分布,X~N(3,4),Y~N(2,9),求D(3X＋4Y)=()
设随机变量X和Y都服从正态分布,则().A.X+Y一定服从正态分布B.(X,Y)一定服从二维正态分布C.X与Y不相关,则X,Y相互独立D.若X与Y相互独立,则X-Y服从正态分布
设二维随机变量(X，Y)服从二维正态分布，则随机变量ζ=X+Y与η=X-Y不相关的充分必要条件为
设(X,Y)服从二维正态分布,其边缘分布为X～N(1,1),Y～N(2,4),X,Y的相关系数为=-0.5,且P(aX+bY≤1)=0.5,则( ).
设随机变量X,Y相互独立,且X～N,Y～N,则与Z=Y-X同分布的随机变量是().A.X-YB.X+YC.X-2YD.Y-2X
设随机变量X,Y都是正态变量,且X,Y不相关,则( ).A.X,Y一定相互独立B.(X,Y)一定服从二维正态分布C.X,y不一定相互独立D.X+y服从一维正态分布
设随机变量X,Y,Z相互独立,且X～U［-1,3］,Y～B,Z～N(1,3……2),且随机变量U=X+2Y-32+2,则D(U)=_______.
设随机变量X服从正态分布N(μ，σ^2)，(σ>0)且二次方程y^2+4y+X=0无实根的概率为，则μ=________.
设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=,则P（X>1,Y>-2）=_______.
设随机变量X,Y相互独立,且X～N(0,4),Y的分布律为Y～.则P(X-1-2Y≤4)=_______.
设二维随机变量(X，Y)服从正态分布N(μ，μ；σ^2，σ^2；0)，则E(XY^2)=________.
设二维随机变量(X，Y)服从正态分布N(1，0;1，1;0)，则P{XY-Y
设随机变量(X，Y)服从二维正态分布，其概率密度为f(x,y)=1/2π
已知随机变量X服从正态分布N(μ，σ2)，设随机变量Y=2X，那么Y服从的分布是()。A.N(2μ，2σ2)B.N(4μ，4σ2)C.N(2μ，4σ2)D.N(μ，σ2)
设随机变量X，Y相互独立，且X～N(μ，σ2)，Y在[a，b]区间上服从均匀分布，则D(X-2Y)=()。
设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。
设随机变量X服从正态分布N（μ1，σ21），随机变量Y服从正态分布N（μ2，σ22），且P{|X-μ1|1}P{|Y-μ2|1}，则必有（）A、σ1σ2B、σ1σ2C、μ1μ2D、μ1μ2
设X，Y是相互独立的随机变量，X~N（2，σ2），Y~N（-3，σ2），且P{|2X+Y-1|≤8.7654}=0.95，则σ=（）。
若随机变量X与Y相互独立，且X服从N（1，9），Y服从N（2，6），则X+Y服从（）分布。
若随机变量X～N（0，4），Y～N（－1，5），且X与Y相互独立。设Z＝X＋Y－3，则Z～（）。
填空题设随机变量X服从正态分布N（μ，σ2）（σ＞0），且二次方程y2＋4y＋X＝0无实根的概率为0.5，则μ＝____。
单选题设随机变量X～N（0，1），Y～N（0，4），且相关系数ρXY=1，则（ ）.AP{Y=-2X-1}=1BP{Y=2X-1}=1CP{Y=-2X+1}=1DP{Y=2X+1}=1
单选题设随机变量X服从正态分布N（μ1，σ12），Y服从正态分布N（μ2，σ22），且P{|X－μ1|＜1}＞P{|Y－μ2|＜1}，则必有（ ）。Aσ1＜σ2Bσ1＞σ2Cμ1＜μ2Dμ1＞μ2
单选题设随机变量（X，Y）服从二维正态分布，且X与Y不相关，fX（x），fY（y）分别表示X，Y的概率密度，则在Y＝y的条件下，X的条件概率密度fX|Y（x|y）为（ ）。AfX（x）BfY（y）CfX（x）fY（y）DfX（x）/fY（y）
,又设Z=
；(3)X,Z是否相互独立？为什么？
