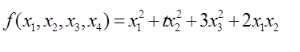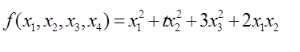设函数,要使f(x)在点x=1处连续,则a的值应是:A.-2B.-1C.0D.1
设矩阵,已知矩阵A相似于B,则秩(A-2E)与秩(A-E)之和等于A.2B.3C.4D.5
要使得二次型为正定的,则t的取值条件是:A. -1B. -1C. t>0D. t
设二次型要使f的秩为2,则参数t的值等于( )。A.3B.2C.1D.0
设参数方程 ,确定了y是x的函数,f''(t)存在且不为零,则d2y/dx2的值是:
设参数方程确定了y是x的函数,且f(t)存在,f(0) = 2,f(0) = 2,则当t=0时,dy/dx的值等于:A. 4/3 B. -4/3 C. -2 D. 2
设则秩r(AB-A)等于:(A) 1(B) 2(C) 3(D)与a的取值有关
设函数要使f(x)在点x=1处连续,则a的值应是:A.-2 B.-1 C.0 D.1
设n阶实对称矩阵A的秩为r,且满足,求 ①二次型的标准形; ②行列式的值,其中E为单位矩阵
设二次型f(x1,x2,x3)=(a>0)的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.
已知,二次型的秩为2. (Ⅰ)求实数a的值; (Ⅱ)求正交变换将二次型化为标准型
设α,β为三维列向量,矩阵A=αα^T+ββ^T,其中α^T,β^T分别是α,β的转置.证明: (Ⅰ)秩r(A)≤2; (Ⅱ)若α,β线性相关,则秩r(A)
要使得二次型f(x1,x2 ,x3)=x12+2tx1x2+x22-2x1x3+2x2x3+2x32 为正定的,则t的取值条件是:A.-10 D.t
参数方程确定了y是x的函数,且f,(t)存在,f(0) = 2, f,(0) = 2,则当t=0时,dy/dx的值等于( )。A. 4/3 B. -4/3 C. -2 D. 2
设f(0)=0,f(1)=16,f(2)=46,则f[0,1]=(),f[0,1,2]=(),f(x)的二次牛顿插值多项式为()。
设3阶方阵A的秩R(A)=1,则A的伴随矩阵的秩R()等于().A、3B、2C、1D、0
设,,则秩r(AB-A)等于()。A、1B、2C、3D、与α的取值有关
已知5阶对称阵A的特征值为-1,0,0,1,1,则二次型f=xTAx的秩等于().A、1B、3C、4D、5
设向量组A:α1=(t,1,1),α2=(1,t,1),α3=(1,1,t)的秩为2,则t等于().A、1B、-2C、1或-2D、任意数
单选题设,,则秩r(AB-A)等于()。A1B2C3D与α的取值有关
单选题设3阶方阵A的秩R(A)=1,则A的伴随矩阵的秩R()等于().A3B2C1D0
填空题设f(0)=0,f(1)=16,f(2)=46,则f[0,1]=(),f[0,1,2]=(),f(x)的二次牛顿插值多项式为()。
单选题设向量组A:α1=(t,1,1),α2=(1,t,1),α3=(1,1,t)的秩为2,则t等于().A1B-2C1或-2D任意数
单选题已知5阶对称阵A的特征值为-1,0,0,1,1,则二次型f=xTAx的秩等于().A1B3C4D5
填空题设α(→)=(1,0,-1,2)T,β(→)=(0,1,0,2),矩阵A=α(→)·β(→),则秩r(A)=____。
单选题设α(→)1,α(→)2,…,α(→)s和β(→)1,β(→)2,…,β(→)t为两个n维向量组,且秩(α(→)1,α(→)2,…,α(→)s)=秩(β(→)1,β(→)2,…,β(→)t)=r,则( )。A此两个向量组等价B秩(α(→)1,α(→)2,…,α(→)s,β(→)1,β(→)2,…,β(→)t)=rC当α(→)1,α(→)2,…,α(→)s可以由β(→)1,β(→)2,…,β(→)t线性表示时,此二向量组等价Ds=t时,二向量组等价